【题目】已知二次函数的解析式为
．
写这个二次函数图象的对称轴和顶点坐标，并求图象与
轴的交点坐标；
在给定的坐标系中画出这个二次函数大致图象，并求出抛物线与坐标轴的交点所组成的三角形的面积．
【答案】（1）对称轴为直线x=1，顶点坐标为（1，2），抛物线与x轴的交点坐标为（1+
，0）、（1﹣，0）；（2）
【解析】
（1）把二次函数y=﹣x2+2x+1化为顶点式的形式，便可直接解答，令y=0，则可求得抛物线与x轴的交点坐标；
（2）由（1）中函数图象与横坐标的交点可求出AB两点之间的距离，再由函数图象与y轴的交点即可求出△ABC的高，由三角形的面积公式即可求解．
（1）∵y=﹣x2+2x+1=﹣（x﹣1）2+2，∴对称轴为直线x=1，顶点坐标为（1，2），令y=0，则x1=1+，x2=1﹣，∴抛物线与x轴的交点坐标为（1+，0）、（1﹣，0）；
（2）二次函数的图象如图所示，设抛物线与x轴的交点坐标为A和B，与y轴的交点为C．
∵A（1﹣，0）、B（1+，0）；
∴AB=2，OC=1，∴S△ABC=
ABOC=×2×1=．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，以△ABC的边AB、AC为边向外作等边三角形△ABD与△ACE，线段BE交DC于点F，下列结论：①CD＝BE；②FA平分∠BAC；③∠BFC＝120°，④FA+FB＝FD，其中正确有（ ）个．
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目：初中数学 来源： 题型：
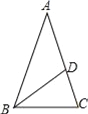
【题目】如图，在△ABC中，AB=AC=1，BC=
，在AC边上截取AD=BC，连接BD．
（1）通过计算，判断AD2与ACCD的大小关系；
（2）求∠ABD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】李大妈加盟了“红红”全国烧烤连锁店，该公司的宗旨是“薄利多销”，经市场调查发现，当羊肉串的单价定为
元时，每天能卖出
串，在此基础上，每加价
元李大妈每天就会少卖出
串，考虑了所有因素后李大妈的每串羊肉串的成本价为
元，若李大妈每天销售这种羊肉串想获得利润是
元，那么请问这种羊肉串应怎样定价？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场用24000元购入一批空调，然后以每台3000元的价格销售，因天气炎热，空调很快售完；商场又以52000元的价格再次购入该种型号的空调，数量是第一次购入的2倍，但购入的单价上调了200元，售价每台也上调了200元．
（1）商场第一次购入的空调每台进价是多少元？
（2）商场既要尽快售完第二次购入的空调，又要在这两次空调销售中获得的利润率不低于22%，打算将第二次购入的部分空调按每台九五折出售，最多可将多少台空调打折出售？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】国家为支持大学生创业，提供小额无息贷款，学生王芳享受政策无息贷款
元用来代理品牌服装的销售．已知该品牌服装进价每件
元，日销售
（件）与销售价
（元/件）之间的关系如图所示（实线），每天付员工的工资每人每天
元，每天应支付其它费用
元．
求日销售（件）与销售价（元/件）之间的函数关系式；
若暂不考虑还贷，当某天的销售价为
元/件时，收支恰好平衡（收入
支出），求该店员工人数；
若该店只有
名员工，则该店至少需要多少天才能还清贷款，此时，每件服装的价格应定为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在某市开展的环境创优活动中，某居民小区要在一块靠墙（墙长
米）的空地上修建一个矩形花园
，花园的一边靠墙，另三边用总长为
的栅栏围成，若设花园平行于墙的一边长为
，花园的面积为
．
求
与
之间的函数关系式，并写出自变量的取值范围；
满足条件的花园面积能达到
吗？若能，求出此时的值，若不能，说明理由；
根据中求得的函数关系式，判断当取何值时，花园的面积最大，最大面积是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当PC与PE的和最小时，∠CPE的度数是_____________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知等腰三角形△ABC，BC边上的高恰好等于BC边长的一半，则∠BAC的度数是（ ）
A.75°B.90°或75°C.90°或 75°或15°D.75°或15°或60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com