
【题目】如图,以△ABC的边AB、AC为边向外作等边三角形△ABD与△ACE,线段BE交DC于点F,下列结论:①CD=BE;②FA平分∠BAC;③∠BFC=120°,④FA+FB=FD,其中正确有( )个.

A.4个B.3个C.2个D.1个
【答案】B
【解析】
证明△ADC≌△ABE,根据全等三角形的性质可推出①③正确,在DF上取一点K,使得FK=FA,可得△AKF是等边三角形,再证明△DAK≌△BAF,可推出④正确,证明AF平分∠DFE,根据三角形外角的性质可推出②不一定成立,故②错误.
解:如图设AC交BE于点O.
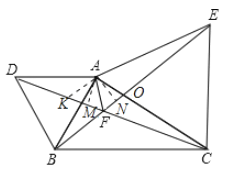
∵△ABD,△ACE都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°,
∴∠DAC=∠EAB,
∴△ADC≌△ABE(SAS),
∴CD=BE,∠AEB=∠ACD,∠ABE=∠ADC,故①正确
作AM⊥CD于M,AN⊥BE于N,
∵△ADC≌△ABE,
∴AM=AN,
∴AF平分∠DFE,∠DFA=∠EFA,
在△ABF和△AFC中,
∠BAF=∠EFA-∠ABF,∠CAF=∠DFA-∠ACD,
∵∠ACD和∠ABF不一定相等,
∴无法判断∠BAF和∠CAF相等,即无法判断AF平分∠BAC,故②错误,
∵∠AOE=∠COF,
∴∠OAE=∠OFC=60°,
∴∠BFC=120°,故③正确,
在DF上取一点K,使得FK=FA,
∵∠AFK=∠AFN=60°,
∴△AKF是等边三角形,
∴AF=AK, ∠DAB=∠KAF =60°
∴∠DAK=∠BAF
又∵AB=AD
∴△DAK≌△BAF(SAS),
∴DK=BF,
∴DF=DK+KF=FA+FB,故④正确,
故①③④正确选:B.


科目:初中数学 来源: 题型:
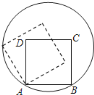
【题目】如图,边长为![]() 的正方形
的正方形![]() 的顶点
的顶点![]() 、
、![]() 在一个半径为
在一个半径为![]() 的圆上,顶点
的圆上,顶点![]() 、
、![]() 在圆内,将正方形
在圆内,将正方形![]() 沿圆的内壁逆时针方向作无滑动的滚动.当点
沿圆的内壁逆时针方向作无滑动的滚动.当点![]() 第一次落在圆上时,点
第一次落在圆上时,点![]() 运动的路径长为________.
运动的路径长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.
(1)请写出二次函数y=2(x-2)2+1的“对称二次函数”;
(2)已知关于x的二次函数y1=x2-3x+1和y2=ax2+bx+c,若y1-y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当-3≤x≤3时,y2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC与BD相交于点O,∠DAB=∠CBA,添加下列哪一个条件后,仍不能使△ADB≌△CBA的是( )

A.AD=BCB.∠ABD=∠BACC.OA=OBD.AC=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,以O为圆心,以任意长为半径作弧,分别交OA,OB于F,E两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证:△FMO≌△FMD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.

(1)求∠AGF的度数;
(2)连接DG,若AG=3、BG=2,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 轴上两点,其中
轴上两点,其中![]() 与
与![]() 互为相反数.点
互为相反数.点![]() 是第二象限内一点,且
是第二象限内一点,且![]() ,点
,点![]() 是直线
是直线![]() 上一动点;
上一动点;
(1)若![]() ,且
,且![]() 是等腰三角形,求
是等腰三角形,求![]() 的度数;
的度数;
(2)点![]() 在直线
在直线![]() 上运动过程中,当
上运动过程中,当![]() 最短时,求
最短时,求![]() 的大小.
的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知长方形ABCD的两个顶点A(2,﹣1),C(6,2),点M为y轴上一点,△MAB的面积为6.请解答下列问题:
(1)顶点B的坐标 ;
(2)连接BD,求BD的长;
(3)请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的解析式为![]() .
.
![]() 写这个二次函数图象的对称轴和顶点坐标,并求图象与
写这个二次函数图象的对称轴和顶点坐标,并求图象与![]() 轴的交点坐标;
轴的交点坐标;
![]() 在给定的坐标系中画出这个二次函数大致图象,并求出抛物线与坐标轴的交点所组成的三角形的面积.
在给定的坐标系中画出这个二次函数大致图象,并求出抛物线与坐标轴的交点所组成的三角形的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com