
����Ŀ�����������κ���ͼ��Ķ�����ͬ�����ڴ�С��ͬ�������ڷ����෴��������������κ���Ϊ���Գƶ��κ�������
(1)��д�����κ���y��2(x��2)2��1�ġ��Գƶ��κ�������
(2)��֪����x�Ķ��κ���y1��x2��3x��1��y2��ax2��bx��c����y1��y2��y1��Ϊ���Գƶ��κ�����������y2�ı���ʽ�����������3��x��3ʱ��y2�����ֵ��
���𰸡�(1) y����2(x��2)2��1��
(2) ![]() .
.
��������
��1���������Գƶ��κ������Ķ��弴����⣻
��2������y1-y2��y1��Ϊ���Գƶ��κ��������������y2�ı���ʽ��Ȼ����y2�ı���ʽת��Ϊ����ʽ�������ö��κ��������ʾͿ��Խ�����⣮
(1)���κ���y��2(x��2)2��1�ġ��Գƶ��κ�������y����2(x��2)2��1��
(2)��y1��x2��3x��1��y2��ax2��bx��c��
��y1��y2��(1��a)x2��(3��b)x��1��c��(1��a)��[x��![]() ]��
]��![]() .
.
��y1��y2��y1��Ϊ���Գƶ��κ�������y1��x2��3x��1��(x��![]() )2��
)2��![]() ��
��
��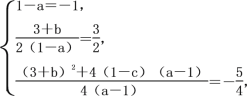 ���
���
��y2��2x2��6x��![]() ��
��
��y2��2(x��![]() )2��
)2��
��y2�ĶԳ���Ϊֱ��x��![]() ��
��
��2��0���ң�3��x��3��
�൱x����3ʱ��y2���ֵ��2��(��3)2��6��(��3)��![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y=��![]() x+b��ͼ�����A��0��3������p�Ǹ�ֱ���ϵ�һ�����㣬����P�ֱ���PM��ֱx���ڵ�M��PN��ֱy���ڵ�N�����ı���PMON�Ϸֱ��ȡ��PC=
x+b��ͼ�����A��0��3������p�Ǹ�ֱ���ϵ�һ�����㣬����P�ֱ���PM��ֱx���ڵ�M��PN��ֱy���ڵ�N�����ı���PMON�Ϸֱ��ȡ��PC=![]() MP��MB=
MP��MB=![]() OM��OE=
OM��OE=![]() ON��ND=
ON��ND=![]() NP��
NP��
��1��b=������
��2����֤���ı���BCDE��ƽ���ı��Σ�
��3����ֱ��y=��![]() x+b���Ƿ���������ĵ�P��ʹ�ı���BCDEΪ�����Σ������ڣ���������з��ϵĵ�P�����ꣻ�������ڣ���˵�����ɣ�
x+b���Ƿ���������ĵ�P��ʹ�ı���BCDEΪ�����Σ������ڣ���������з��ϵĵ�P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABC�У���ABC=45�㣬CD��AB��D��BEƽ�֡�ABC����BE��AC��E����CD�ཻ�ڵ�F��H��BC�ߵ��е㣬����DH��BE�ཻ�ڵ�G.
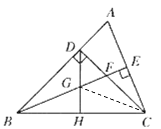
(1)��֤��BF=AC��
(2)��֤��CE=![]() BF��
BF��
(3)CE��BG�Ĵ�С��ϵ��Σ���֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֱ�д������1��2��3�����ſ�Ƭ��ע�������ſ�Ƭ����״����С���ʵأ���ɫ������������ȫ��ͬ���������Ϸ��������ϣ������ſ�Ƭ����ȥ���κβ��ϴ�Ⱥ������Ϸ��������ϣ������������ȡһ�ſ�Ƭ���Ǹÿ�Ƭ�ϵ�����Ϊx���ٰ�ʣ�µ����ſ�Ƭϴ�Ⱥ������Ϸ��������ϣ��ٴ������ſ�Ƭ�������ȡһ�ſ�Ƭ���Ǹÿ�Ƭ�ϵ�����Ϊy��
��1�����б�������״ͼ������״ͼҲ������ͼ���е�һ�ַ�����д����x��y�����п��ܳ��ֵĽ����
��2����ȡ�������ſ�Ƭ�ϵ�����֮��Ϊż���ĸ���P��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н����п�����ʵ��������ԣ�����ѧ����ǩ��ʽ�����Լ��Ŀ������ݣ��涨��ÿλ������������������ʵ��(��ֽǩA��B��C��ʾ)��������ѧʵ��(��ֽǩD��E��F��ʾ)�и���ȡһ�����п��ԣ�С���ڿ�����ֽǩ������£��ֱ���и������ȡһ����
(1) �á��б���������״ͼ������ʾ���п��ܳ��ֵĽ����
(2) С�ճ鵽����ʵ��B�ͻ�ѧʵ��F(�����¼�P)�ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����AC�ǡ�O�����ߣ��ڡ�O��ȡ��D������CD��ʹ��AC=CD���ӳ�CD��ֱ��AB�ڵ�E��
(1)��֤��CD�ǡ�O�����ߣ�
(2)��AC=2![]() ��AE=6��
��AE=6��
�����O�İ뾶��
�ڵ�M���Ż�![]() �ϵ�һ�����㣨����B��D�غϣ�����MD��MB����BDΧ�ɵ���Ӱ������������ֵ��
�ϵ�һ�����㣨����B��D�غϣ�����MD��MB����BDΧ�ɵ���Ӱ������������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧ���Դ�ѧϰ��̬��һֱ�ǽ��������߹�ע������֮һ��Ϊ�ˣ�ij����ί�Ը�������ѧУ�İ��꼶ѧ���Դ�ѧϰ��̬�Ƚ�����һ�γ������飨��ѧϰ̬�ȷ�Ϊ�����㼶��A������ѧϰ�ܸ���Ȥ��B������ѧϰ�ϸ���Ȥ��C������ѧϰ������Ȥ�����������������Ƴ�ͼ����ͼ����ͳ��ͼ�����������������ͼ���ṩ����Ϣ������������⣺

��1���˴γ��������У��������� ��ѧ����
��2����ͼ������������
��3�����ͼ����C����ռ��Բ�ĽǵĶ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�ı�AB��ACΪ���������ȱ���������ABD����ACE���߶�BE��DC�ڵ�F�����н��ۣ���CD��BE����FAƽ�֡�BAC���ۡ�BFC��120������FA+FB��FD��������ȷ�У�����������

A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC=1��BC=![]() ����AC���Ͻ�ȡAD=BC������BD��
����AC���Ͻ�ȡAD=BC������BD��
��1��ͨ�����㣬�ж�AD2��ACCD�Ĵ�С��ϵ��
��2�����ABD�Ķ�����
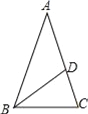
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com