
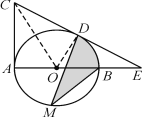
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,在⊙O上取点D,连接CD,使得AC=CD,延长CD交直线AB于点E.
(1)求证:CD是⊙O的切线.
(2)若AC=2![]() ,AE=6.
,AE=6.
①求⊙O的半径.
②点M是优弧![]() 上的一个动点(不与B,D重合),求MD,MB及弧BD围成的阴影部分面积的最大值.
上的一个动点(不与B,D重合),求MD,MB及弧BD围成的阴影部分面积的最大值.

【答案】(1)见解析;(2)①⊙O的半径为2,②![]() π+2
π+2
【解析】
(1)连结OD,OC.根据SSS可证△CAO≌△CDO,得∠ODC=∠OAC=90°,则CD是 O的切线;
(2)①由(1)的结论可以得到CD=CA,再依据勾股定理可以求得 O的半径为2;
②面积可看成两部分,三角形DMB跟弧DB的面积,弧DB不变,三角形面积为底DB乘以高除以2,当M运动到优弧![]() 的中点时,阴影部分的面积最大,可求得最大值.
的中点时,阴影部分的面积最大,可求得最大值.
(1)证明:连接OD,OC,如图.
∵AC是⊙O的切线,
∴∠CAB=90°,
在△CAO和△CDO中
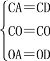 ,
,
∴△CAO≌△CDO.
∴∠CAO=∠CDO=90°,
∴CD⊥OD,
∴CD是⊙O的切线.
(2)解: ①∵AC=2![]() ,AE=6,
,AE=6,
∴根据勾股定理得:CE=4![]() ,
,
又∵AC=CD,∴DE=2![]() ,
,
∴∠CEA=30°,
∴tan∠CEA=![]() =
=![]() ,
,
∴OD=2.
∴⊙O的半径为2.
②∵图中阴影部分的面积可看成两部分,△DMB的面积和弓形DB的面积,
∵弧DB不变,∴三角形底边DB不变,
当M运动到优弧![]() 的中点,高最大,即面积最大.
的中点,高最大,即面积最大.
由(1)及第(2)①得:∠DOB=60°,当M运动到优弧![]() 的中点时,此时高经过圆心且垂直于DB,所以高的值为2+
的中点时,此时高经过圆心且垂直于DB,所以高的值为2+![]() ,
,
又△DOB是等边三角形,∴DB=OB=2,
∴S△DBM=![]() ×2×(2+
×2×(2+![]() )=2+
)=2+![]() ,
,
又因为S弓形DB=S扇形ODB-S△ODB=![]() -
-![]() =
=![]() -
-![]() ,
,
∴图中阴影部分的面积为:S=S弓形DB+S△DBM=![]() π+2.
π+2.


科目:初中数学 来源: 题型:
【题目】山西皮影戏又称“影戏”或“影子戏”,属于传统民间艺术,皮影是一种以兽皮或纸板做成的人物剪影,在制作人物剪影中,给出下面4个条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.

(1)在上述四个条件中,选三个条件作为题设,另一个作为结论,其中真命题有哪几个?(用序号表示即可)
(2)请选择(1)中的一个命题证明其正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx﹣3的图象经过点A,且函数值y随x的增大而增大,则点A的坐标不可能是( )
A.(﹣2,﹣4)B.(﹣1,2)C.(5,1)D.(﹣1,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.
(1)请写出二次函数y=2(x-2)2+1的“对称二次函数”;
(2)已知关于x的二次函数y1=x2-3x+1和y2=ax2+bx+c,若y1-y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当-3≤x≤3时,y2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC与BD相交于点O,∠DAB=∠CBA,添加下列哪一个条件后,仍不能使△ADB≌△CBA的是( )

A.AD=BCB.∠ABD=∠BACC.OA=OBD.AC=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.

(1)求∠AGF的度数;
(2)连接DG,若AG=3、BG=2,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com