
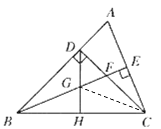
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF;
BF;
(3)CE与BG的大小关系如何?试证明你的结论.
【答案】(1)证明见解析;(2)证明见解析;(3)CE<BG.证明见解析.
【解析】
(1)证明△BDF≌△CDA,得到BF=AC;(2)由(1)问可知AC=BF,所以CE=AE=![]() BF;(3) BG=CG,CG在△EGC中,CE<CG.
BF;(3) BG=CG,CG在△EGC中,CE<CG.
解:(1)证明:因为CD⊥AB, ∠ABC=45°,
所以△BCD是等腰直角三角形.
所以BD=CD.
在Rt△DFB和Rt△DAC中,
因为∠DBF=90°-∠BFD, ∠DCA=90°-∠EFC,
又∠BFD=∠EFC,
所以∠DBF=∠DCA.
又因为∠BDF=∠CDA=90°,BD=CD,.
所以Rt△DFB≌Rt△DAC.
所以BF=AC.
(2)证明:在Rt△BEA和Rt△BEC中,
因为BE平分∠ABC,
所以∠ABE=∠CBE.
又因为BE=BE, ∠BEA=∠BEC=90°,
所以Rt△BEA≌Rt△BEC.
所以CE=AE=![]() AC.
AC.
又由(1),知BF=AC,
所以CE=![]() AC=
AC=![]() BF.
BF.
(3)CE<BG.证明:连接CG,
因为△BCD是等腰直角三角形,
所以BD=CD,
又H是BC边的中点,
所以DH垂直平分BC.
所以BG=CG,
在Rt△CEG中,
因为CG是斜边,CE是直角边,
所以CE<CG,即CE<BG.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】(1)已知:如图1,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥BF.
(2)如图2所示,△ABC的顶点分别为A(﹣4,5),B(﹣3,2),C(4,﹣1)
①作出△ABC关于x轴对称的图形△A1B1C1;
②用三角板作出△ABC的AB边上的高CH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
我们知道“两边及其中一边的对角分别对应相等的两个三角形不一定全等”.但是,乐乐发现:当这两个三角形都是锐角三角形时,它们会全等.
(1)请你用所学知识判断乐乐说法的正确性.
如图,已知![]() 、
、![]() 均为锐角三角形,且
均为锐角三角形,且![]() ,
,![]() ,
,![]() .
.
求证:![]() .
.

(2)除乐乐的发现之外,当这两个三角形都是______时,它们也会全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形
的正方形![]() 的顶点
的顶点![]() 、
、![]() 在一个半径为
在一个半径为![]() 的圆上,顶点
的圆上,顶点![]() 、
、![]() 在圆内,将正方形
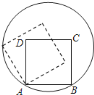
在圆内,将正方形![]() 沿圆的内壁逆时针方向作无滑动的滚动.当点
沿圆的内壁逆时针方向作无滑动的滚动.当点![]() 第一次落在圆上时,点
第一次落在圆上时,点![]() 运动的路径长为________.
运动的路径长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx﹣3的图象经过点A,且函数值y随x的增大而增大,则点A的坐标不可能是( )
A.(﹣2,﹣4)B.(﹣1,2)C.(5,1)D.(﹣1,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点E,F在边AB上,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处.

(1)求∠ECF的度数;
(2)若CE=4,B'F=1,求线段BC的长和△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.
(1)请写出二次函数y=2(x-2)2+1的“对称二次函数”;
(2)已知关于x的二次函数y1=x2-3x+1和y2=ax2+bx+c,若y1-y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当-3≤x≤3时,y2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 轴上两点,其中
轴上两点,其中![]() 与
与![]() 互为相反数.点
互为相反数.点![]() 是第二象限内一点,且
是第二象限内一点,且![]() ,点
,点![]() 是直线
是直线![]() 上一动点;
上一动点;
(1)若![]() ,且
,且![]() 是等腰三角形,求
是等腰三角形,求![]() 的度数;
的度数;
(2)点![]() 在直线
在直线![]() 上运动过程中,当
上运动过程中,当![]() 最短时,求
最短时,求![]() 的大小.
的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com