
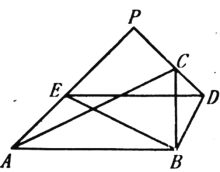
【题目】如图,在![]() 与
与![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,射线
,射线![]() 与直线
与直线![]() 交于点P.
交于点P.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 绕点B逆时针旋转一周,直接写出线段
绕点B逆时针旋转一周,直接写出线段![]() 的最大值与最小值.
的最大值与最小值.
【答案】(1)证明见详解;(2)![]() ;(3)
;(3)![]() ,3
,3![]() -
-![]() .
.
【解析】
(1)由![]() ,∠ABE =∠CBD,结合
,∠ABE =∠CBD,结合![]() ,即可得证;
,即可得证;
(2)过点E作EM⊥AB,则EM=BN=2,BM=EN=5-1=4,易证:∴PED,CND,AME都是等腰直角三角形,根据正切三角函数的定义,即可求解;
(3)由![]() ,易证:点P,C,B,A在以AC为直径的圆弧上,结合图形,可得线段
,易证:点P,C,B,A在以AC为直径的圆弧上,结合图形,可得线段![]() 的最大值与最小值.
的最大值与最小值.
(1)∵![]() ,
,
∴∠ABE=∠ABC-∠EBC=∠EBD-∠EBC=∠CBD,
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴DE=5,
∵![]() ,
,
∴BN⊥DE,
∴BN=![]() ,
,
∴CN=BC-BN=3-2=1,![]() ,
,
∴CN=DN,
∴∠PDE=45°,
过点E作EM⊥AB,则EM=BN=2,BM=EN=5-1=4,如图1,
∴AM=6-4=2,
∴AM=EM,
∴∠EAB=45°,
∴∠PED=∠EAB=45°,
∴PED,CND,AME都是等腰直角三角形,
∴PE=PD=5÷![]() =
=![]() ,AE=2
,AE=2![]() ,CD=
,CD=![]() ,
,
∴PA=PE+AE=![]() ,PC= PD- CD=
,PC= PD- CD=![]() ,
,
∴![]() =
=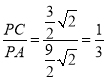 ;
;
(3)∵![]() ,如图1,
,如图1,
∴∠EAB=∠DCB,
∵∠DCB+∠PCB=180°,
∴∠EAB +∠PCB=180°,
∴点P,C,B,A在以AC为直径的圆弧上,
∴AP≤AC=![]() ,
,
∴AP的最大值为:![]() .
.
当![]() 且都是等腰直角三角形时,AP的值最小,如图2,
且都是等腰直角三角形时,AP的值最小,如图2,
此时,![]() 都是等腰直角三角形,
都是等腰直角三角形,
设AP=x,则AM=![]() ,MB=6-
,MB=6-![]() ,
,
∵![]()
∴![]() ,解得:x=3
,解得:x=3![]() -
-![]() ,
,
即:AP的最小值为:3![]() -
-![]() ./span>
./span>
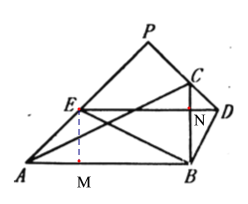
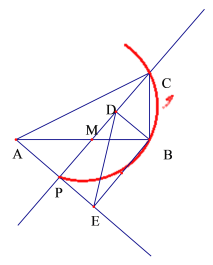
图1 图2


科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,线段AB的端点坐标分别为A(0,6)、B(6,6).点Q在线段AB上,以Q为项点的抛物线y=﹣![]() x2+bx+c与y轴交于点D,与x轴的一个交点为C.设点Q的横坐标为m,点C的横坐标为n(n>m).
x2+bx+c与y轴交于点D,与x轴的一个交点为C.设点Q的横坐标为m,点C的横坐标为n(n>m).
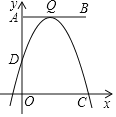
(1)当m=0时,求n的值.
(2)求线段AD的长(用含m的式子表示);
(3)点P(2,0)在x轴上,设△BPD的面积为S,求S与m的关系式;
(4)当△DCQ是以QC为直角边的直角三角形时,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
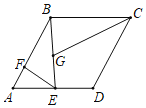
【题目】如图,菱形ABCD的边长是6,∠A=60°,E是AD的中点,F是AB边上一个动点,EG=EF且∠GEF=60°,则GB+GC的最小值是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年,国家卫生健康委员会和国家教育部在全国开展了儿童青少年近视调查工作,调查数据显示,全国儿童青少年近视过半.某校初三学习小组为了解本校学生对自己视力保护的重视程度,随机在校内调查了部分学生,调查结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成下面的两幅不完整的统计图:
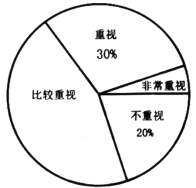
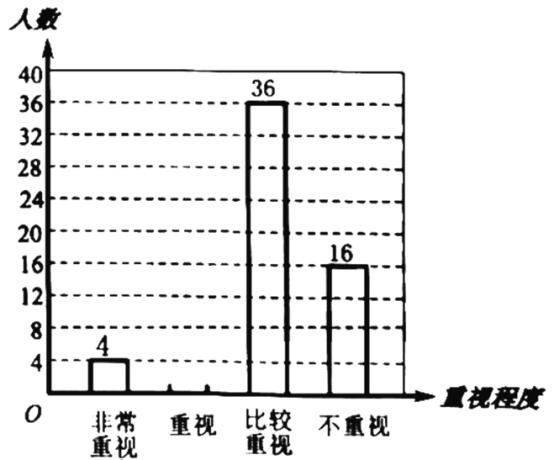
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)该校共有学生1000人,请你估计该校对视力保护“非常重视”的学生人数;
(3)对视力“非常重视”的4人有![]() ,
,![]() 两名男生,
两名男生,![]() ,
,![]() 两名女生,若从中随机抽取两人向全校作视力保护交流,请利用树状图或列表的方法,求恰好抽到一男一女的概率.
两名女生,若从中随机抽取两人向全校作视力保护交流,请利用树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=![]() (x>0)的图象上,点D的坐标为(4,3).
(x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)将这个菱形沿x轴正方向平移,当顶点D落在反比例函数图象上时,求菱形平移的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克30元,规定每千克售价不低于成本,且不高于70元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 50 | 60 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
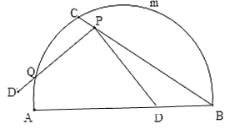
【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
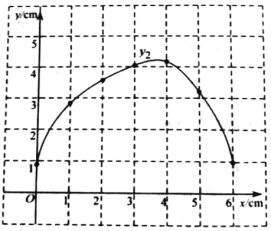
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com