
【题目】已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE.
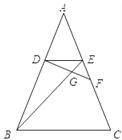
求证:(1)△DEF∽△BDE;(2)DGDF=DBEF.
【答案】证明:(1)∵AB=AC,∴∠ABC=∠ACB.…………………………………………1分
∵DE∥BC,∴∠ABC+∠BDE=180°,∠ACB+∠CED=180°.
∴∠BDE=∠CED. …………………………………………1分
∵∠EDF=∠ABE,∴△DEF∽△BDE.…………………………………………1分
(2)由△DEF∽△BDE,得![]() .
.
∴![]() . …………………………………………1分
. …………………………………………1分
由△DEF∽△BDE,得∠BED=∠DFE.
∵∠GDE=∠EDF,∴△GDE∽△EDF.…………………………………1分
∴![]() . …………………………………………1分
. …………………………………………1分
∴![]() . …………………………………………1分
. …………………………………………1分
∴![]() . …………………………………………1分
. …………………………………………1分
【解析】略


科目:初中数学 来源: 题型:
【题目】如图,A,B,C三点在⊙O上,且AB是⊙O的直径,半径OD⊥AC,垂足为F,若∠A=30,OF=3,则OA=_____,AC=_____,BC=_____.
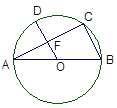
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的有 ( )个
①40°角为内角的两个等腰三角形必相似
②若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为750
③一组对边平行,另一组对边相等的四边形是平行四边形
④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2∶b2∶c2=2∶1∶1
⑤若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c,则此△为等腰直角三角形。
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=-2x经过点P(-2,m),点P关于y轴的对称点P′在反比例函数![]() (
(![]() )的图象上.
)的图象上.
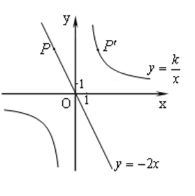
(1)求m的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )

A. 8:1B. 6:1C. 5:1D. 4:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程kx2﹣(4k+1)x+3k+3=0(k是整数).
(1)求证:方程有两个不相等的实数根;
(2)若方程的两个实数根都是整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高考英语听力测试期间,需要杜绝考点周围的噪音。如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的![]() 点处有一消防队。在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火。已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶。试问:消防车是否需要改道行驶?说明理由.(
点处有一消防队。在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火。已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶。试问:消防车是否需要改道行驶?说明理由.(![]() 取1.732)
取1.732)
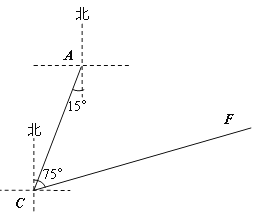
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c的三项系数分别为a、b、c,则定义[a,b,c]为该函数的“特征数”.如:函数y=x2+3x-2的“特征数”是[1,3,-2],函数y=-x+4的“特征数”是[0,-1,4].如果将“特征数”是[2,0,4]的函数图象向左平移3个单位,得到一个新的函数图象,那么这个新图象相应的函数表达式是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
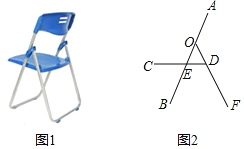
【题目】如图1,是一种折叠椅,忽略其支架等的宽度,得到它的侧面简化结构图(图2),支架与坐板均用线段表示.若坐板CD平行于地面,前支撑架AB与后支撑架OF分别与CD交于点E,D,ED=25cm,OD=20cm,DF=40cm,∠ODC=60°,∠AED=50°.
(1)求两支架着地点B,F之间的距离;
(2)若A、D两点所在的直线正好与地面垂直,求椅子的高度.
(结果取整数,参数数据:sin60°=0.87,cos60°=0.5,tan60°=1.73,sin50°=0.77,cos50°=0.64,tan50°=1.19)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com