
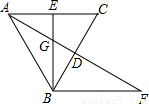
已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC, BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F, DF=6.
(1) 求AE的长;
(2) 求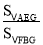 的值.
的值.
(1)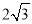 ;(2)
;(2)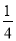 .
.
【解析】
试题分析:(1)根据等边三角形的性质和判定推出∠C=60°,求出∠CBF=60°,∠F=30°,解直角三角形求出BD,即可得出答案.
(2)求出BF长,根据相似三角形的性质和判定得出即可.
试题解析:(1)∵在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC,
∴AC=AB=BC.∴△ABC是等边三角形.∴∠C=60°.
∵BF∥AC,∴∠CBF=∠C=60°.
∵AD⊥BC,∴∠FDB=90°.∴∠F=30°.
∵DF=6,∴BD=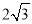 .
.
∵AE=EC=BD=DC,∴AE=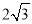 .
.
(2)∵∠BDF=90°,∠F=30°,BD=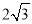 ,∴BF=2DB=
,∴BF=2DB=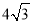 .
.
∵AC∥BF,∴△AEG∽△FBG.
∴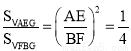 .
.
考点:1.等边三角形的判定与性质;2.相似三角形的判定与性质.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源:2014年北京市房山区中考二模数学试卷(解析版) 题型:解答题
已知关于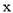 的一元二次方程
的一元二次方程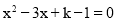 有实数根,
有实数根,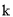 为正整数.
为正整数.
(1)求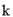 的值;
的值;
(2)当此方程有两个不为0的整数根时,将关于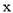 的二次函数
的二次函数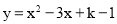 的图象向下平移2个单位,求平移后的函数图象的解析式;
的图象向下平移2个单位,求平移后的函数图象的解析式;
(3)在(2)的条件下,将平移后的二次函数图象位于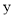 轴左侧的部分沿
轴左侧的部分沿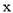 轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线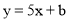 与图象G有3个公共点时,请你直接写出
与图象G有3个公共点时,请你直接写出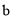 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考二模数学试卷(解析版) 题型:选择题
如果二次函数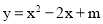 的最小值为负数,则m的取值范围是( )
的最小值为负数,则m的取值范围是( )
A.m﹤1 B.m﹥1 C.m≤1 D.m≥1
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:解答题
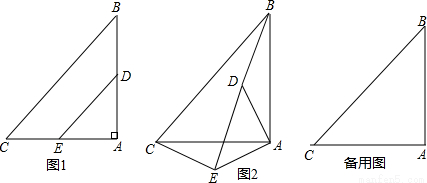
将等腰Rt△ABC和等腰Rt△ADE按图1方式放置,∠A=90°, AD边与AB边重合, AB=2AD=4.将△ADE绕点A逆时针方向旋转一个角度α(0°≤α≤180°),BD的延长线交直线CE于点P.
(1)如图2,BD与CE的数量关系是 , 位置关系是 ;
(2)在旋转的过程中,当AD⊥BD时,求出CP的长;
(3)在此旋转过程中,求点P运动的路线长.[
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:解答题
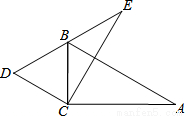
已知:如图,在△DBC中,BC=DC,过点C作CE⊥DC交DB的延长线于点E,过点C作AC⊥BC且AC=EC,连结AB.
求证:AB=ED.
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:选择题
如图,在边长为9的正方形ABCD中, F为AB上一点,连接CF.过点F作FE⊥CF,交AD于点E,若AF=3,则AE等于( )
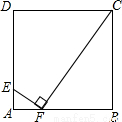
A.1 B.1.5 C.2 D.2.5
查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:解答题
如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.
(1)当点D′恰好落在EF边上时,求旋转角α的值;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值;若不能说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com