
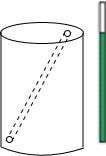
 如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置)
如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置) 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
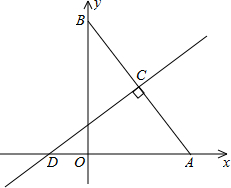 如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴、y轴的正半轴上(OA<OB﹚,且AO,OB的长分别是一元二次方程x2-14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,交x轴于点D,D的坐标为(-
如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴、y轴的正半轴上(OA<OB﹚,且AO,OB的长分别是一元二次方程x2-14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,交x轴于点D,D的坐标为(-| 3 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
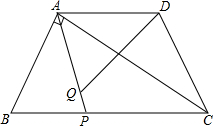 如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60°
如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60°查看答案和解析>>
科目:初中数学 来源: 题型:
| A、相等 | B、互补 |
| C、相等或互补 | D、相等或互余 |
查看答案和解析>>
科目:初中数学 来源: 题型:
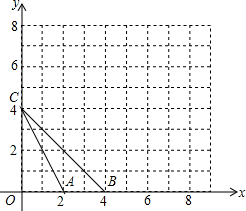 如图,在平面直角坐标系中,△ABC的顶点坐标为A(2,0)、B(4,0)、C(0,4),将各顶点的横坐标、纵坐标都乘2,得相应的点A′、B′、C′的坐标.
如图,在平面直角坐标系中,△ABC的顶点坐标为A(2,0)、B(4,0)、C(0,4),将各顶点的横坐标、纵坐标都乘2,得相应的点A′、B′、C′的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
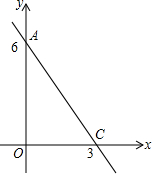 已知直线l:y=kx+b经过点A(0,6)且平行于直线y=-2x
已知直线l:y=kx+b经过点A(0,6)且平行于直线y=-2x查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com