
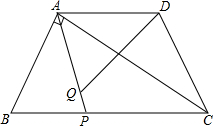
 如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60°
如图,等腰梯形ABCD中,AB=CD,AD∥BC,AD=2,BC=4,∠B=60°,如果P是BC上一点,Q是AP上一点,且∠AQD=60°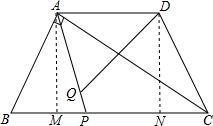
| AD |
| AP |
| DQ |
| AB |
| 2 |
| x |
| y |
| 2 |
| 4 |
| x |
| BC2-AB2 |
| 42-22 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
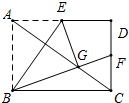 在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.
在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
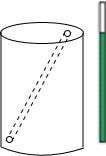 如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置)
如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置)查看答案和解析>>
科目:初中数学 来源: 题型:
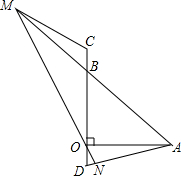 如图,已知△ABO是等腰直角三角形,OB=OA,C、D在直线BO上,BC=OD,ON⊥AD,垂足是N,AB、NO的延长线交于M,连接MC,求证:∠C+∠D=180°.
如图,已知△ABO是等腰直角三角形,OB=OA,C、D在直线BO上,BC=OD,ON⊥AD,垂足是N,AB、NO的延长线交于M,连接MC,求证:∠C+∠D=180°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com