练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．如图，AB是⊙O的直径，弦CD与AB相交，且∠ABC=32°，则∠CDB的度数为（　　）
    A．58°B．32°C．80°D．64°

    分析 由AB是⊙O的直径，可得知∠ACB=90°，根据三角形内角和为180°可求出∠BAC的度数，再由同弦的圆周角相等得出结论．

    解答 解：∵线段AB为⊙O的直径，
    ∴∠ACB=90°，
    ∴∠BAC=180°-∠ACB-∠ABC=58°．
    ∵∠CDB与∠BAC均为弦BC的圆周角，
    ∴∠CDB=∠BAC=58°．
    故选A．

    点评 本题考查了三角形的内角和以及圆周角的定理，解题的关键是找到弦BC的另一个圆心角∠BAC的度数．本题属于基础题，难度不大，做形如此类题时，要寻找同弦的圆周角或者圆心角．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．计算：|-5|-（-4）2+（-2）3÷4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．已知二次函数y=ax2+2x+c（a≠0）有最大值，且ac=2，则二次函数的顶点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．当x=-3时，代数式x-2x2的值是-21．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．某河流中的水位在某天规定的时间测得的数据记录如下（规定上升为正，单位：cm）：3，-6，-1，5，-4，2，-3，-2，求这天中河流最终水位比原来水位上升（或下降）了多少cm？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

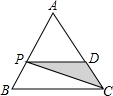    5．如图，P为等边三角形ABC中AB边上的动点，沿A→B的方向运动，到达点B时停止，过P作PD∥BC．设AP=x，△PDC的面积为y，则y关于x的函数图象大致为（　　）
    A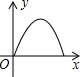．B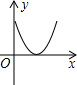．C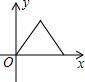．D．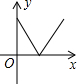

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．思考探究
    思考．
    （1）计算：$\sqrt{{2}^{2}}$=2；$\sqrt{（-\frac{2}{3}）^{2}}$=$\frac{2}{3}$；$\sqrt{{0}^{2}}$=0．
    （2）计算：（$\sqrt{2}$）2=2；（$\sqrt{\frac{2}{3}}$）2=$\frac{2}{3}$；（$\sqrt{0}$）2=0．
    探究
    （3）对于任意实数a，$\sqrt{{a}^{2}}$=|a|．
    （4）对于任意非负实数a，（$\sqrt{a}$）2=a．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．某校综合实践活动小组与5月20日（中国学生营养日）开展快餐营养情况调查活动，他们在互联网查获的食品安全监督部门的一份快餐信息如图所示，请根据此信息，解答下列问题：
    （1）求这份快餐中脂肪的含量；
    （2）若碳水化合物占快餐总质量的40%，求这份快餐所含蛋白质和矿物质的质量；
    （3）若这份快餐中蛋白质和碳水化合物所占百分比之和不超过84%，求其中所含碳水化合物质量的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

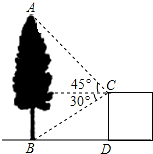    18．如图，在建筑平台CD的顶部C处，测得大树AB的顶部A的仰角为45°，测得大树AB的底部B的俯角为30°，已知平台CD的高度为5m，求大树的高度．

    查看答案和解析>>

    同步练习册答案