
【题目】如图,直线![]() 经过
经过![]() 的直角顶点
的直角顶点![]() 的边上有两个动点
的边上有两个动点![]() ,点
,点![]() 以
以![]() 的速度从点
的速度从点![]() 出发沿
出发沿![]() 移动到点
移动到点![]() ,点
,点![]() 以
以![]() 的速度从点
的速度从点![]() 出发,沿
出发,沿![]() 移动到点
移动到点![]() ,两动点中有一个点到达终点后另一个点继续移动到终点过点
,两动点中有一个点到达终点后另一个点继续移动到终点过点![]() 分别作
分别作![]()
![]() ,垂足分别为点
,垂足分别为点![]() .若
.若![]() ,设运动时间为
,设运动时间为![]() ,则当
,则当![]() ___
___![]() 时,以点
时,以点![]() 为顶点的三角形与以点
为顶点的三角形与以点![]() 为顶点的三角形全等.
为顶点的三角形全等.

【答案】1或![]() 或
或![]()
【解析】
分当E在BC线段上时,此时D在AC线段上;当E在AC线段上时,且D在AC线段上;当E到达A时,且D在BC线段上,三种情况进行讨论,相应列出方程求解即可.
解:当E在BC线段上时,此时D在AC线段上,
故CE=8-3t,CD=6-t,
当DC=CE时,![]()
故8-3t =6-t
解得:t=1
当E在AC线段上时,且D在AC线段上,
故CE=3t-8,CD=6-t,
当DC=CE时,![]()
故3t-8 =6-t
解得:![]()
当E到达A时,且D在BC线段上,
故CE=6,CD=t-6,
当DC=CE时,![]()
故6 =t-6
解得:![]()
综上所述:t=1或![]() 或
或![]() 时,,以点
时,,以点![]() 为顶点的三角形与以点
为顶点的三角形与以点![]() 为顶点的三角形全等.
为顶点的三角形全等.
故答案为:1或![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共20只,某学习小组作摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表示活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
请估算口袋中白球约是( )只.
A. 8 B. 9 C. 12 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)
如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是
是![]() 轴上的一个动点.当点
轴上的一个动点.当点![]() 在
在![]() 轴上移动时,始终保持
轴上移动时,始终保持![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() (点
(点![]() 、
、![]() 、
、![]() 按逆时针方向排列);当点
按逆时针方向排列);当点![]() 移动到点
移动到点![]() 时,得到等腰直角三角形
时,得到等腰直角三角形![]() (此时点
(此时点![]() 与点
与点![]() 重合).
重合).
(初步探究)
(1)写出点![]() 的坐标______.
的坐标______.
(2)点![]() 在
在![]() 轴上移动过程中,当等腰直角三角形
轴上移动过程中,当等腰直角三角形![]() 的顶点
的顶点![]() 在第四象限时,连接
在第四象限时,连接![]() .
.
求证:![]() ;
;
(深入探究)
(3)当点![]() 在
在![]() 轴上移动时,点
轴上移动时,点![]() 也随之运动.经过探究发现,点
也随之运动.经过探究发现,点![]() 的横坐标总保持不变,请直接写出点
的横坐标总保持不变,请直接写出点![]() 的横坐标:______.
的横坐标:______.
(拓展延伸)
(4)点![]() 在
在![]() 轴上移动过程中,当
轴上移动过程中,当![]() 为等腰三角形时,直接写出此时点
为等腰三角形时,直接写出此时点![]() 的坐标.
的坐标.
 备用图
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,且DM=DN.
(1)如图甲,若∠C=90°,∠BAC=60°,AC=9,∠MDN=120°,ND∥AB.
①写出∠MDA= °,AB的长是 .
②求四边形AMDN的周长;

(2)如图乙,过D作DF⊥AC于F,先补全图乙再证明AM+AN=2AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC 中,点 D 是线段 BC 上一点.作射线 AD ,点 B 关于射线 AD 的对称点为 E .连接 EC 并延长,交射线 AD 于点 F .
(1)补全图形;(2)求∠AFE 的度数;(3)用等式表示线段 AF 、CF 、 EF 之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一块含有![]() 角的三角板放置在一条直线上,
角的三角板放置在一条直线上,![]() 边与直线
边与直线![]() 重合,
重合,![]() 边的垂直平分线与边
边的垂直平分线与边![]() 分别交于
分别交于![]() 两点,连接
两点,连接![]() .
.


(1) ![]() 是 三角形;
是 三角形;
(2)直线![]() 上有一动点
上有一动点![]() (不与点
(不与点![]() 重合) ,连接
重合) ,连接![]() 并把
并把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() .当点
.当点![]() 在图2所示的位置时,证明
在图2所示的位置时,证明![]() .我们可以用
.我们可以用![]() 来证明
来证明![]() ,从而得到
,从而得到![]() .当点
.当点![]() 移动到图3所示的位置时,结论是否依然成立?若成立,请你写出证明过程;若不成立,请你说明理由.
移动到图3所示的位置时,结论是否依然成立?若成立,请你写出证明过程;若不成立,请你说明理由.
(3)当点![]() 在
在![]() 边上移动时(不与点
边上移动时(不与点![]() 重合),
重合),![]() 周长的最小值是 .
周长的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中的任意两点![]() ,
,![]() ,我们把
,我们把![]() 叫
叫![]() ,
,![]() 两点间的“平面距离”,记作
两点间的“平面距离”,记作![]() .
.
(![]() )已知
)已知![]() 为坐标原点,动点
为坐标原点,动点![]() 是坐标轴上的点,满足
是坐标轴上的点,满足![]() ,请写出点
,请写出点![]() 的坐标.答:__________.
的坐标.答:__________.
(![]() )设
)设![]() 是平面上一点,
是平面上一点,![]() 是直线
是直线![]() 上的动点,我们定义
上的动点,我们定义![]() 的最小值叫做
的最小值叫做![]() 到直线
到直线![]() 的“平面距离”.试求点
的“平面距离”.试求点![]() 到直线
到直线![]() 的“平面距离”.
的“平面距离”.
(![]() )在上面的定义基础上,我们可以定义平面上一条直线
)在上面的定义基础上,我们可以定义平面上一条直线![]() 与⊙
与⊙![]() 的“直角距离”:在直线
的“直角距离”:在直线![]() 与⊙
与⊙![]() 上各自任取一点,此两点之间的“平面距离”的最小值称为直线
上各自任取一点,此两点之间的“平面距离”的最小值称为直线![]() 与⊙
与⊙![]() 的“平面距离”,记作
的“平面距离”,记作![]() .
.
试求直线![]() 与圆心在直线坐标系原点、半径是
与圆心在直线坐标系原点、半径是![]() 的⊙
的⊙![]() 的直角距离
的直角距离![]() __________.(直接写出答案)
__________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图,在正方形![]() 和平行四边形
和平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
探究:当![]() 与
与![]() 的夹角为多少度时,平行四边形
的夹角为多少度时,平行四边形![]() 是正方形?
是正方形?
小聪同学的思路是:首先可以说明四边形![]() 是矩形;然后延长
是矩形;然后延长![]() 交
交![]() 于点
于点![]() ,构造全等三角形,经过推理可以探索出问题的答案.
,构造全等三角形,经过推理可以探索出问题的答案.
请你参考小聪同学的思路,探究并解决这个问题.

(1)求证:四边形![]() 是矩形;
是矩形;
(2)![]() 与
与![]() 的夹角为________度时,四边形
的夹角为________度时,四边形![]() 是正方形.
是正方形.
理由:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
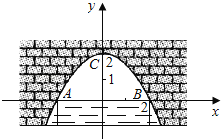
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com