
【题目】如图,正方形纸片ABCD,P为正方形AD边上的一点(不与点A,点D重合),将正方形纸片折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接BP,BH.BH交EF于点M,连接PM.下列结论:①BE=PE;②EF=BP;③PB平分∠APG;④MH=MF;⑤BP=![]() BM,其中正确结论的个数是( )
BM,其中正确结论的个数是( )
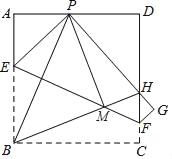
A. 5 B. 4 C. 3 D. 2
【答案】B
【解析】
①③利用正方形的性质、翻折不变性即可解决问题;
②构造全等三角形即可解决问题;
④利用特殊位置,判定结论即可;
⑤只要证明△PBM是等腰直角三角形即可解决问题;
如图1,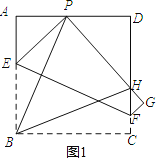
根据翻折不变性可知:PE=BE,
∴∠EBP=∠EPB.
又∵∠EPH=∠EBC=90°,
∴∠EPH-∠EPB=∠EBC-∠EBP.
即∠PBC=∠BPH.
又∵AD∥BC,
∴∠APB=∠PBC.
∴∠APB=∠BPH.故①③正确;
如图1中,作FK⊥AB于K.设EF交BP于O.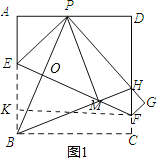
∵∠FKB=∠KBC=∠C=90°,
∴四边形BCFK是矩形,
∴KC=BC=AB,
∵EF⊥PB,
∴∠BOE=90°,
∵∠ABP+∠BEO=90°,∠BEO+∠EFK=90°,
∴∠ABP=∠EFK,∵∠A=∠EKF=90°,
∴△ABP≌△KFE(ASA),
∴EF=BP,故②正确,
如图2,过B作BQ⊥PH,垂足为Q.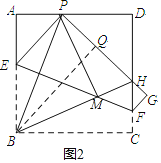
由(1)知∠APB=∠BPH,
在△ABP和△QBP中,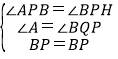 ,
,
∴△ABP≌△QBP(AAS).
∴AP=QP,AB=BQ.
又∵AB=BC,
∴BC=BQ.
又∵∠C=∠BQH=90°,BH=BH,
∴△BCH≌△BQH(HL)
∴∠QBH=∠HBC,∠ABP=∠PBQ,
∴∠PBH=∠PBQ+∠QBH=![]() ∠ABC=45°,
∠ABC=45°,
∵MP=MB,
∴△PBM是等腰直角三角形,
∴PB=![]() BM,故⑤正确;
BM,故⑤正确;
当等P与A重合时,显然MH>MF,故④错误,
故选:B.


科目:初中数学 来源: 题型:
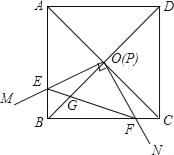
【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,直角∠MPN的顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是_____.
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(4)OGBD=AE2+CF2.
;(4)OGBD=AE2+CF2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦今年一月份销售额为![]() 万元,二月份由于种种原因,经营不善,销售额下降
万元,二月份由于种种原因,经营不善,销售额下降![]() ,以后加强改进管理,经减员增效,大大激发了全体员工的积极性,月销售额大幅度上升,到四月份销售额猛增到
,以后加强改进管理,经减员增效,大大激发了全体员工的积极性,月销售额大幅度上升,到四月份销售额猛增到![]() 万元,求三、四月份平均每月增长的百分率是多少?
万元,求三、四月份平均每月增长的百分率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图反映了初三(1)班、(2)班的体育成绩。

(1)不用计算,根据条形统计图,_______班学生的体育成绩好一些。
(2)从图中观察出:三(1)班学生体育成绩等级的众数是_______;三(2)班学生体育成绩等级的众数是_______.
(3)如果依次将不及格、及格、中、良好、优秀记为55、65、75、85、95分,请你观察计算一下初三(1),(2)班的平均成绩各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲和乙玩一种游戏:从装有大小相同的![]() 个红球和一个黄球的袋子中,任意摸出
个红球和一个黄球的袋子中,任意摸出![]() 球,如果摸到黄球,甲得
球,如果摸到黄球,甲得![]() 分;如果摸到红球,乙得
分;如果摸到红球,乙得![]() 分.
分.
![]() 你认为这个游戏公平吗?
你认为这个游戏公平吗?
![]() 假设玩这个游戏
假设玩这个游戏![]() 次,甲大约得多少分,乙大约得多少分?
次,甲大约得多少分,乙大约得多少分?
![]() 如果你认为游戏不公平,那么怎样修改得分标准才公平?
如果你认为游戏不公平,那么怎样修改得分标准才公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____.
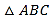
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种成本为![]() 元
元![]() 的水产品,若按
的水产品,若按![]() 元
元![]() 销售,一个月可售出
销售,一个月可售出![]() ,售价毎涨
,售价毎涨![]() 元,月销售量就减少
元,月销售量就减少![]() .
.
![]() 写出月销售利润
写出月销售利润![]() (元)与售价
(元)与售价![]() (元
(元![]() )之间的函数表达式;
)之间的函数表达式;
![]() 当售价定为多少元时,该商店月销售利润为
当售价定为多少元时,该商店月销售利润为![]() 元?
元?
![]() 当售价定为多少元时会获得最大利润?求出最大利润.
当售价定为多少元时会获得最大利润?求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点,延长BC至点F,使CF=CE.
(1)∠ABC的度数.
(2)求证:BE=FE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com