
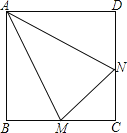
【题目】如图,M、N分别是正方形ABCD的边BC、CD上的点,已知:∠MAN=30°,AM=AN,△AMN的面积为1.
(1)求∠BAM的度数;
(2)求正方形ABCD的边长.
【答案】(1)∠BAM=30°;(2)正方形ABCD的边长为![]() .
.
【解析】
(1)只要证明△ABM≌△ADN(HL),推出∠BAM=∠DAN,由∠MAN=30°,∠BAD=90°,即可推出∠BAM=30°;
(2)作MH⊥AN于H.设BM=x,则AM=AN=2x,MH=x,根据![]() ANMH=1,列出方程即可;
ANMH=1,列出方程即可;
解:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=∠BAD=90°,
∵AM=AN,
在Rt△ABM和Rt△ADN中,
![]() ,
,
∴△ABM≌△ADN(HL),
∴∠BAM=∠DAN,
∵∠MAN=30°,∠BAD=90°,
∴∠BAM=30°.
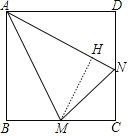
(2)作MH⊥AN于H.设BM=x,则AM=AN=2x,MH=x,
∵![]() ANMH=1,
ANMH=1,
∴![]() 2xx=1,
2xx=1,
解得x=1或﹣1(舍弃),
∴AB=![]() BM=
BM=![]() ,
,
∴正方形ABCD的边长为![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
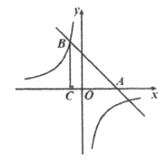
【题目】如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 的一个交点为B(-1,4).
的一个交点为B(-1,4).
(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线![]() 上,且△PAC的面积为4,求点P的坐标.
上,且△PAC的面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() 出现了错误,解答过程如下:
出现了错误,解答过程如下:
方程两边都乘以![]() ,得
,得![]() (第一步)
(第一步)
去括号,得![]() (第二步)
(第二步)
移项,合并同类项,得![]() (第三步)
(第三步)
解得![]() (第四步)
(第四步)
![]() 原方程的解为
原方程的解为![]() (第五步)
(第五步)
(1)小明解答过程是从第_____步开始出错的,这一步正确的解答结果_____,此步的根据是_____.
(2)小明的解答过程缺少_____步骤,此方程的解为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
尺规作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.

小云的作法如下:
(1)在直线l上任取一点B;
(2)以B为圆心,BA长为半径作弧,交直线l于点C;
(3)分别以A、C为圆心,BA长为半径作弧,两弧相交于点D;
(4)作直线AD.直线AD即为所求.

小云作图的依据是_______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2-12ax+36a-5的图象在4<x<5这一段位于x轴下方,在8<x<9这一段位于x轴上方,则a的值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)
(1)观察下列算式,并完成填空:
1=12
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+…+(2n-1)=______.(n是正整数)
(2)如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.
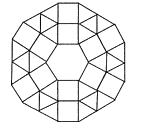
①第3层中分别含有______块正方形和______块正三角形地板砖;
②第n层中含有______块正三角形地板砖(用含n的代数式表示).
(应用)
该市打算在一个新建广场中央,采用如图样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E为长方形纸片ABCD的边CD上一点,将纸片沿AE对折,点D的对应点D′恰好在线段BE上.若AD=3,DE=1,则AB=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=﹣2x2+4x+m+1,与x轴的公共点为A,B.
(1)如果A与B重合,求m的值;
(2)横、纵坐标都是整数的点叫做整点:
①当m=﹣1时,求线段AB上整点的个数;
②若设抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,当1<n≤8时,结合函数的图象,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com