
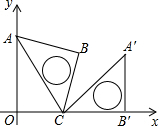
 将一个含45°角的三角板ABC如图摆放在平面直角坐标系中,将其绕点C顺时针旋转75°,点B的对应点B′恰好落在x轴上,若点C的坐标为(1,0),则点B′的坐标为(1+$\sqrt{2}$,0).
将一个含45°角的三角板ABC如图摆放在平面直角坐标系中,将其绕点C顺时针旋转75°,点B的对应点B′恰好落在x轴上,若点C的坐标为(1,0),则点B′的坐标为(1+$\sqrt{2}$,0). 分析 先求得∠ACO=60°,得出∠OAC=30°,求得AC=20C=2,解等腰直角三角形求得直角边为$\sqrt{2}$,从而求出B′的坐标.
解答 解:如图,∵∠ACB=45°,∠BCB′=75°,
∴∠ACB′=120°,
∴∠ACO=60°,
∴∠OAC=30°,
∴AC=2OC,
∵点C的坐标为(1,0),
∴OC=1,
∴AC=2OC=2,
∵△ABC是等腰直角三角形,
∴AB=BC=$\sqrt{2}$,
∴B′C=A′B′=$\sqrt{2}$,
∴OB′=1+$\sqrt{2}$,
∴B′点的坐标为(1+$\sqrt{2}$,0).
点评 此题主要考查了旋转的性质及坐标与图形变换,同时也利用了直角三角形性质,首先利用直角三角形的性质得到有关线段的长度,即可解决问题.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:解答题
 在一年一度的国家学生体质侧试中,金星中学对全饺2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图.
在一年一度的国家学生体质侧试中,金星中学对全饺2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图.| 序号 | 范围(单位:秒) | 频数 | 频率 |
| 1 | 170<x≤200 | 5 | 0.1 |
| 2 | 200<x≤230 | 13 | a |
| 3 | 230<x≤260 | 15 | 0.3 |
| 4 | 260<x≤290 | c | d |
| 5 | 290<x≤320 | 5 | 0.1 |
| 6 | 320<x≤350 | 2 | 0.04 |
| 7 | 350<x≤380 | 2 | 0.04 |
| 合计 | b | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.0×105 | B. | 30×104 | C. | 3.0×104 | D. | 3.0×101 |
查看答案和解析>>
科目:初中数学 来源:2017届江西省高安市九年级下学期第一次模拟考试数学试卷(解析版) 题型:判断题
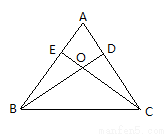
如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O,
(1)求证:OB=OC
(2)如果∠ABC=50o,求∠BOC的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com