
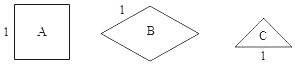
【题目】将图中的![]() 型(正方形)、
型(正方形)、![]() 型(菱形)、
型(菱形)、![]() 型(等腰直角三角形)纸片分别放在
型(等腰直角三角形)纸片分别放在![]() 个盒子中,盒子的形状、大小、质地都相同,再将这
个盒子中,盒子的形状、大小、质地都相同,再将这![]() 个盒子装入一只不透明的袋子中.
个盒子装入一只不透明的袋子中.
(1)搅匀后从中摸出![]() 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
(2)搅匀后先从中摸出![]() 个盒子(不放回),再从余下的
个盒子(不放回),再从余下的![]() 个盒子中摸出
个盒子中摸出![]() 个盒子,把摸出的
个盒子,把摸出的![]() 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
【答案】(1)![]() ;(2)见解析,
;(2)见解析,![]() .
.
【解析】
(1)依据搅匀后从中摸出![]() 个盒子,可能为
个盒子,可能为![]() 型(正方形)、
型(正方形)、![]() 型(菱形)或
型(菱形)或![]() 型(等腰直角三角形)这
型(等腰直角三角形)这![]() 种情况,其中既是轴对称图形又是中心对称图形的有
种情况,其中既是轴对称图形又是中心对称图形的有![]() 种,即可得到盒中的纸片既是轴对称图形又是中心对称图形的概率;
种,即可得到盒中的纸片既是轴对称图形又是中心对称图形的概率;
(2)依据共有![]() 种等可能的情况,其中拼成的图形是轴对称图形的情况有
种等可能的情况,其中拼成的图形是轴对称图形的情况有![]() 种:
种:![]() 和
和![]() ,
,![]() 和
和![]() ,即可得到拼成的图形是轴对称图形的概率.
,即可得到拼成的图形是轴对称图形的概率.
(1)搅匀后从中摸出![]() 个盒子,可能为
个盒子,可能为![]() 型(正方形)、
型(正方形)、![]() 型(菱形)或
型(菱形)或![]() 型(等腰直角三角形)这
型(等腰直角三角形)这![]() 种情况,其中既是轴对称图形又是中心对称图形的有
种情况,其中既是轴对称图形又是中心对称图形的有![]() 种,
种,
![]() 盒中的纸片既是轴对称图形又是中心对称图形的概率是
盒中的纸片既是轴对称图形又是中心对称图形的概率是![]() ;
;
故答案为:![]() ;
;
(2)画树状图为:
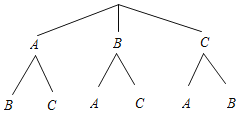
共有![]() 种等可能的情况,其中拼成的图形是轴对称图形的情况有
种等可能的情况,其中拼成的图形是轴对称图形的情况有![]() 种:
种:![]() 和
和![]() ,
,![]() 和
和![]() ,
,
![]() 拼成的图形是轴对称图形的概率为
拼成的图形是轴对称图形的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过
经过![]() 三点,抛物线的顶点为点
三点,抛物线的顶点为点![]() ,对称轴与
,对称轴与![]() 轴的交点为点
轴的交点为点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,连接
,连接![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作圆,点
的长为半径作圆,点![]() 为直线
为直线![]() 上的一个动点.
上的一个动点.
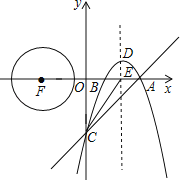
(1)求抛物线的解析式;
(2)求![]() 周长的最小值;
周长的最小值;
(3)若动点![]() 与点
与点![]() 不重合,点
不重合,点![]() 为⊙
为⊙![]() 上的任意一点,当
上的任意一点,当![]() 的最大值等于
的最大值等于![]() 时,过
时,过![]() 两点的直线与抛物线交于
两点的直线与抛物线交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),求四边形
的左侧),求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某菜市场有2.5平方米和4平方米两种摊位,2.5平方米的摊位数是4平方米摊位数的2倍.管理单位每月底按每平方米20元收取当月管理费,该菜市场全部摊位都有商户经营且各摊位均按时全额缴纳管理费.
(1)菜市场毎月可收取管理费4500元,求该菜市场共有多少个4平方米的摊位?
(2)为推进环保袋的使用,管理单位在5月份推出活动一:“使用环保袋送礼物”,2.5平方米和4平方米两种摊位的商户分别有40%和20%参加了此项活动.为提高大家使用环保袋的积极性,6月份准备把活动一升级为活动二:“使用环保袋抵扣管理费”,同时终止活动一.经调査与测算,参加活动一的商户会全部参加活动二,参加活动二的商户会显著增加,这样,6月份参加活动二的2.5平方米摊位的总个数将在5月份参加活动一的同面积个数的基础上增加2a%,毎个摊位的管理费将会减少![]() ;6月份参加活动二的4平方米摊位的总个数将在5月份参加活动一的同面积个数的基础上增加6a%,每个摊位的管理费将会减少
;6月份参加活动二的4平方米摊位的总个数将在5月份参加活动一的同面积个数的基础上增加6a%,每个摊位的管理费将会减少![]() .这样,参加活动二的这部分商户6月份总共缴纳的管理费比他们按原方式共缴纳的管理费将减少
.这样,参加活动二的这部分商户6月份总共缴纳的管理费比他们按原方式共缴纳的管理费将减少![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
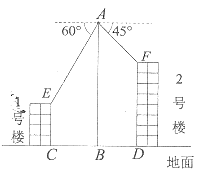
【题目】综合实践课上,某兴趣小组同学用航拍无人机进行测高实践,如图为实践时绘制的截面图.无人机从地面点![]() 垂直起飞到达点
垂直起飞到达点![]() 处,测得学校1号楼顶部
处,测得学校1号楼顶部![]() 的俯角为
的俯角为![]() ,测得2号楼顶部
,测得2号楼顶部![]() 的俯角为
的俯角为![]() ,此时航拍无人机的高度为50米.已知1号楼的高度为20米,且
,此时航拍无人机的高度为50米.已知1号楼的高度为20米,且![]() 和
和![]() 分别垂直地面于点
分别垂直地面于点![]() 和
和![]() ,
,![]() 为
为![]() 的中点,求2号楼的高度(结果保留根号).
的中点,求2号楼的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万kg与3.6万kg,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率;
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万kg.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线y=-x2+bx+c经过A(0,-2),B(-1,1)两点,那么此抛物线经过
A. 第一、二、三、四象限 B. 第一、二、三象限
C. 第一、二、四象限 D. 第二、三、四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
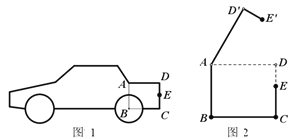
【题目】如图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD'E'的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D'到BC的距离;
(2)求E、E'两点的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com