
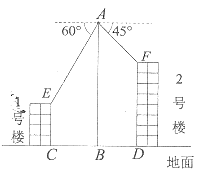
【题目】综合实践课上,某兴趣小组同学用航拍无人机进行测高实践,如图为实践时绘制的截面图.无人机从地面点![]() 垂直起飞到达点
垂直起飞到达点![]() 处,测得学校1号楼顶部
处,测得学校1号楼顶部![]() 的俯角为
的俯角为![]() ,测得2号楼顶部
,测得2号楼顶部![]() 的俯角为
的俯角为![]() ,此时航拍无人机的高度为50米.已知1号楼的高度为20米,且
,此时航拍无人机的高度为50米.已知1号楼的高度为20米,且![]() 和
和![]() 分别垂直地面于点
分别垂直地面于点![]() 和
和![]() ,
,![]() 为
为![]() 的中点,求2号楼的高度(结果保留根号).
的中点,求2号楼的高度(结果保留根号).
 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
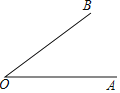
【题目】已知:![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:
①以![]() 为圆心,任意长为半径画弧,分别交
为圆心,任意长为半径画弧,分别交![]() ,
,![]() 于点
于点![]() ;
;
②画一条射线![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ;
;
③以点![]() 为圆心,
为圆心,![]() 长为半径画弧,与第②步中所画的弧相交于点
长为半径画弧,与第②步中所画的弧相交于点![]() ;
;
④过点![]() 画射线
画射线![]() ,则
,则![]() .
.
根据上面的作法,完成以下问题:
(1)使用直尺和圆规,作出![]() (请保留作图痕迹).
(请保留作图痕迹).
(2)完成下面证明![]() 的过程(注:括号里填写推理的依据).
的过程(注:括号里填写推理的依据).
证明:由作法可知![]() ,
,![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ( )
( )
∴![]() .( )
.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某海监船以60海里/时的速度从A处出发沿正西方向巡逻,一可疑船只在A的西北方向的C处,海监船航行1.5小时到达B处时接到报警,需巡査此可疑船只,此时可疑船只仍在B的北偏西![]() 方向的C处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速以90海里/时的速度追击,在D处海监船追到可疑船只,D在B的北偏西
方向的C处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速以90海里/时的速度追击,在D处海监船追到可疑船只,D在B的北偏西![]() 方同.(以下结果保留根号)
方同.(以下结果保留根号)
(1)求B,C两处之问的距离;
(2)求海监船追到可疑船只所用的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
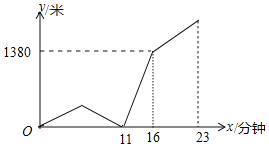
【题目】一天,小明从家出发匀速步行去学校上学.几分钟后,在家休假的爸爸发现小明忘带数学书,于是爸爸立即匀速跑步去追小明,爸爸追上小明后以原速原路跑回家.小明拿到书后以原速的![]() 快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小明家到学校的路程为________米.
快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小明家到学校的路程为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a<0)经过点(-1,0),且满足4a+2b+c>0.以下结论(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图中的![]() 型(正方形)、
型(正方形)、![]() 型(菱形)、
型(菱形)、![]() 型(等腰直角三角形)纸片分别放在
型(等腰直角三角形)纸片分别放在![]() 个盒子中,盒子的形状、大小、质地都相同,再将这
个盒子中,盒子的形状、大小、质地都相同,再将这![]() 个盒子装入一只不透明的袋子中.
个盒子装入一只不透明的袋子中.
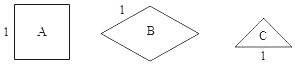
(1)搅匀后从中摸出![]() 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
(2)搅匀后先从中摸出![]() 个盒子(不放回),再从余下的
个盒子(不放回),再从余下的![]() 个盒子中摸出
个盒子中摸出![]() 个盒子,把摸出的
个盒子,把摸出的![]() 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数:![]() .
.
(1)求证:二次函数的图象与x轴有两个交点;
(2)当二次函数的图象与x轴的两个交点的横坐标均为整数,且a为负整数时,求a的值及二次函数的解析式并画出二次函数的图象(不用列表,只要求用其与x轴的两个交点A,B(A在B的左侧),与y轴的交点C及其顶点D这四点画出二次函数的大致图象,同时标出A,B,C,D的位置);
(3)在(2)的条件下,二次函数的图象上是否存在一点P使![]() ?如果存在,求出点P的坐标;如果不存在,请说明理由.
?如果存在,求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在⊙O的直径AB延长线上,点C在⊙O上,过点D作ED⊥AD,与AC的延长线相交于点E,且CD=DE.
(1)求证:CD为⊙O的切线;
(2)若AB=12,且BC=CE时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com