
����Ŀ���ҹ��Ŵ���ѧ������ֶ���λ������ǰ�У���������Ǿ���һ������ͼ����������εĹ��취�������ϵ�������1������ÿ������Ϊ���Ϸ���������֮�ͣ��������ˣ�a+b��n��nΪ����������չ��ʽ����a�Ĵ����������У���ϵ���������磬���������е�һ�е�������1��2��1��ǡ�ö�Ӧ��a+b��2��a2+2ab+b2չ��ʽ�е�ϵ���������е��ĸ���1��3��3��1��ǡ�ö�Ӧ�ţ�a+b��3��a3+3ab+3ab2+b3չ��ʽ�е�ϵ������϶�������ǵ����������������
��1����a+b��2չ��ʽa2+2ab+b2��ÿһ��Ĵ��������� ���Σ�
��a+b��3չ��ʽa3+3a2b+3ab2+b3��ÿһ��Ĵ��������� ���Σ�
��ô��a+b��nչ��ʽ��ÿһ��Ĵ��������� ���Σ�
��2��д����a+1��4��չ��ʽ�� ����
��3����չӦ�ã����㣨x+1��5+��x��1��6+��x+1��7�Ľ���У�x5���ϵ��Ϊ�� ����
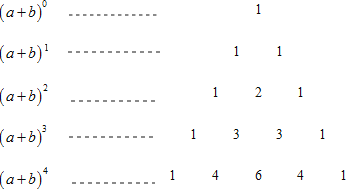
���𰸡���1��2��3��n����2��a4+4a3b+6a2b2+4ab3+b4��3��16.
��������
��1���۲죨a+b��2չ��ʽ�ͣ�a+b��3չ��ʽ�и�����ɵô𰸣��Ӷ��Ƴ���a+b��n��չ���
��2�������������ͼ�п�֪��a+1��4��չ��ʽ�ĸ���ϵ�������ɵý⣻
��3����x+1��5��x5���ϵ��Ϊ1���ٰ�������ǣ��ֱ���ã�x��1��6�ͣ�x+1��7չ��ʽ��x5���ϵ��������ϵ����Ӽ��ɵô𰸣�
�⣺��1����a+b��2չ��ʽa2+2ab+b2�е���ֱ�Ϊ��a2��2ab��b2�����ǵĴ�������2��
��a+b��3չ��ʽa3+3a2b+3ab2+b3�е���ֱ�Ϊ��a3��3a2b��3ab2��b3�����ǵĴ�������3��
�ɴ��Ƴ���a+b��nչ��ʽ�Ĵ�������n��
�ʴ�Ϊ��2��3��n��
��2�������������ͼ�п�֪��a+1��4��չ��ʽ�ĸ���ϵ���ֱ�Ϊ��1��4��6��4��1��չ��ʽΪ����a+1��4��a4+4a3b+6a2b2+4ab3+b4��
�ʴ�Ϊ��a4+4a3b+6a2b2+4ab3+b4��
��3����x+1��5��x5���ϵ��Ϊ1��
����������ǿ�֪��x��1��6��x6+6x5����1��+��+1����x+1��7��x7+7x6��1+21x5��12+��+1��
�ࣨx+1��5+��x��1��6+��x+1��7�Ľ���У�x5���ϵ��Ϊ��1+6������1��+21��16
�ʴ�Ϊ��16��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BAC��90������B��30����BC������һ��P�������B��C�غϣ���IΪ��APC�����ģ�����AIC��ȡֵ��ΧΪm������AIC��n������m+n��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����������أ����ĵױ�BC=100�ף���AH=80�ף�ij��λҪ���ŵر�BC��һ�������Ǿ���DEFG�Ĵ�¥��D��G�ֱ���AB��AC�ı��ϣ��ʵ��������������ʱ�����ij�������Ƕ����ף�������Ϊ����ƽ���ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
�У�![]() ���ֱ���
���ֱ���![]() ��
��![]() ��������������
��������������![]() ��������
��������![]() ��
��
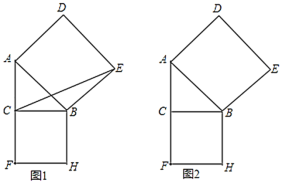
��1����![]() ʱ��������
ʱ��������![]() ���ܳ�=_______���ú�
���ܳ�=_______���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2������![]() ����˵����������
����˵����������![]() ���������������
���������������![]() �����һ�룮
�����һ�룮
��3����֪![]() ���ҵ�
���ҵ�![]() ���߶�
���߶�![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ���߶�
���߶�![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ���
���![]() �����ƶ������У�
�����ƶ������У�![]() ���ܳ��Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵�����ɣ�
���ܳ��Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С������Ϸ����ͼ��������ͬ�Ŀ�Ƭ��ÿ�����ţ���һ�鿨Ƭ����ֱ��������1��3��5���ڶ��鿨Ƭ����ֱ��������2��4��6�����ǽ���Ƭ���泯�ϣ�������ϴ�Ⱥ�ÿ�鿨Ƭ�и�����һ�ţ���Ϊһ����Ϸ�������������ſ�Ƭ����������֮��С��10����С����ʤ�������������ſ�Ƭ����������֮������10����С����ʤ������Ϊ�����Ϸ�����˫����ƽ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Բ���β�������Ϊ12cm�������ܳ�Ϊ18cm���ڱ����뱭��4cm�ĵ�C
����һ�η��ۣ���ʱһֻ���������ڱ���ڣ��뱭����4cm�������Եĵ�A���������ϵ�����۵���
�̾���Ϊ �� cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB��DC��AB��AD���Խ���AC��BD���ڵ�O��ACƽ����BAD������C��CE��AB��AB���ӳ����ڵ�E������OE��
��1����֤���ı���ABCD�����Σ�
��2����AB��![]() ��BD��2����OE�ij���
��BD��2����OE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��E��F�ֱ�Ϊ����ABCD�ı�AD��BC�ϵĵ㣬AE=CF����֤��BE=DF��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com