
【题目】某校准备开春季运动会,学校要给学生买若干笔袋和笔记本作为奖品.购买2个笔袋和1个笔记本需花25元,购买3个笔袋和2个笔记本需花40元.
(1)求笔袋和笔记本的单价各是多少元?
(2)学校准备购买笔袋和笔记本共计180个,甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案,在甲商场累计购物超过1000元后,超出1000元的部分按90%收费,在乙商场累计购物超过500元后,超出500元的部分按95%收费,经过预算此次购物超过了1000元,求学校需要至少购买多少个笔袋,才能使到甲商场购物更省钱?
【答案】(1)笔袋单价为10元,笔记本单价为5元;(2)学校需要购买至少121个笔袋才能使到甲商场购买更省钱.
【解析】
(1)设笔袋单价为![]() 元,笔记本单价为
元,笔记本单价为![]() 元,根据“购买2个笔袋和1个笔记本需花25元,购买3个笔袋和2个笔记本需花40元”可列出二元一次方程组,解方程组即可得出答案.
元,根据“购买2个笔袋和1个笔记本需花25元,购买3个笔袋和2个笔记本需花40元”可列出二元一次方程组,解方程组即可得出答案.
(2)设学校需要购买![]() 个笔袋才能使到甲商场购买更省钱;则学校需要购买
个笔袋才能使到甲商场购买更省钱;则学校需要购买![]() 个笔记本,根据“在甲商场累计购物超过1000元后,超出1000元的部分按90%收费,在乙商场累计购物超过500元后,超出500元的部分按95%收费,经过预算此次购物超过了1000元”列出一元一次不等式,解之即可得出
个笔记本,根据“在甲商场累计购物超过1000元后,超出1000元的部分按90%收费,在乙商场累计购物超过500元后,超出500元的部分按95%收费,经过预算此次购物超过了1000元”列出一元一次不等式,解之即可得出![]() 的取值范围,进而得出
的取值范围,进而得出![]() 的最小整数值.
的最小整数值.
(1)解:设笔袋单价为![]() 元,笔记本单价为
元,笔记本单价为![]() 元。
元。
![]()
解得:![]()
答:笔袋单价为10元,笔记本单价为5元.
(2)设学校需要购买![]() 个笔袋才能使到甲商场购买更省钱;则学校需要购买
个笔袋才能使到甲商场购买更省钱;则学校需要购买![]() 个笔记本;
个笔记本;
学校购买两种物品共需花费![]() 元
元
∵经过预算此次购物超过了1000元
∵![]()
解得:![]()
根据题意可列式为:![]()
解得:![]()
∵![]() 为正整数
为正整数
∴![]() 最小值为121
最小值为121
答;学校需要购买至少121个笔袋才能使到甲商场购买更省钱.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点![]() 、
、![]() ,以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程
,以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程![]() 与时间
与时间![]() 满足关系
满足关系![]() ,乙以
,乙以![]() 的速度匀速运动,半圆的长度为
的速度匀速运动,半圆的长度为![]() .
.
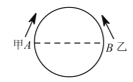
(1)甲运动![]() 后的路程是多少?
后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.
(1)试求点E的坐标(用含m,n的式子表示);
(2)求证:AM=AN;
(3)若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种货物的数量与3月份相同,4月份共收取运费13000元.试求该物流公司3月份运输A、B两种货物各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E.
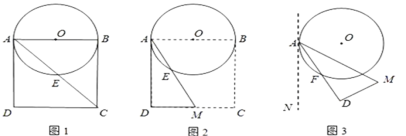
(1)线段AE= ;
(2)如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F.
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α= °时,DM与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),连接
重合),连接![]() 过点
过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .作
.作![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
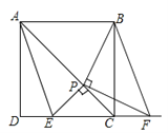
(1)由题意易知,![]() ,观察图,请猜想另外两组全等的三角形
,观察图,请猜想另外两组全等的三角形![]()
![]() ;
;![]()
![]() ;
;
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)已知![]() ,
,![]() 的面积是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是唐初作为“算学”教科书的著名的《算经十书》之一,共三卷,上卷叙述算筹记数的制度和乘除法则,中卷举例说明筹算分数法和开平方法,都是了解中国古代筹算的重要资料,下卷收集了一些算术难题,“鸡兔同笼”便是其中一题.下卷中还有一题,记载为:“今有甲乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八.问甲、乙二人持钱各几何?”意思是:“甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文.如果乙得到甲所有钱的![]() ,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
A.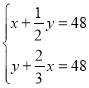 B.
B.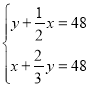 C.
C.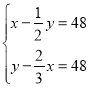 D.
D.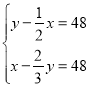
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴分别于点A(﹣3,0),B(1,0),交y轴正半轴于点D,抛物线顶点为C.下列结论
①2a﹣b=0;
②a+b+c=0;
③当m≠﹣1时,a﹣b>am2+bm;
④当△ABC是等腰直角三角形时,a=![]() ;
;
⑤若D(0,3),则抛物线的对称轴直线x=﹣1上的动点P与B、D两点围成的△PBD周长最小值为3![]() ,其中,正确的个数为( )
,其中,正确的个数为( )
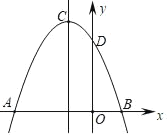
A.2个B.3个C.4个D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com