
����Ŀ��ijУΪ����������Ƽ������������ٰ��˶����������С������˵���Բ���˶���һ�����Σ���ͼ��ʾ���ס�������ֱ��ֱ�������˵�![]() ��
��![]() ����˳ʱ�롢��ʱ��ķ���ͬʱ��Բ���˶������˶���·��
����˳ʱ�롢��ʱ��ķ���ͬʱ��Բ���˶������˶���·��![]() ��ʱ��
��ʱ��![]() �����ϵ
�����ϵ![]() ������
������![]() ���ٶ������˶�����Բ�ij���Ϊ
���ٶ������˶�����Բ�ij���Ϊ![]() ��
��
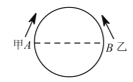
��1�����˶�![]() ���·���Ƕ���?
���·���Ƕ���?
��2���ס��Ҵӿ�ʼ�˶�����һ������ʱ�������˶��˶���ʱ��?
��3���ס��Ҵӿ�ʼ�˶����ڶ�������ʱ�������˶��˶���ʱ��?
���𰸡���1��28cm����2��3s����3��7s
��������
��1����t=4���빫ʽ���㼴�ɣ�
��2����һ���������ǹ��߰�Բ�ij��ȣ��ݴ��з���![]() ����⼴�ɣ�
����⼴�ɣ�
��3���ڶ�������Ӧ������������Բ�ij��ȣ��õ�![]() ���ⷽ�̼��ɵõ���.
���ⷽ�̼��ɵõ���.
�⣺��1���� t=4s ʱ��![]() cm.
cm.
�𣺼��˶� 4s ���·���� ![]() ��
��
��2�� ��ͼ��֪�����ҵ�һ������ʱ�߹���·��Ϊ��Բ ![]() �����߹���·��Ϊ
�����߹���·��Ϊ ![]() ��
��
���߹���·��Ϊ ![]() ����
����![]() .
.
��� ![]() ��
�� ![]() ���������⣬��ȥ����
���������⣬��ȥ����
�𣺼ס��Ҵӿ�ʼ�˶�����һ������ʱ�������˶��� 3s��
��3�� ��ͼ��֪�����ҵڶ�������ʱ�߹���·��Ϊ������Բ ![]() ��
��
��![]()
��� ![]() ��
�� ![]() ���������⣬��ȥ����
���������⣬��ȥ����
�𣺼ס��Ҵӿ�ʼ�˶����ڶ�������ʱ�������˶��� 7s��


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������IJ�����װ��4������1��2��3��4��С�����ǵ���״����С��ȫ��ͬ��С���Ӳ��������ȡ��һ��С��������Ϊ![]() ��С����ʣ�µ�3��С�������ȡ��һ��С��������Ϊ
��С����ʣ�µ�3��С�������ȡ��һ��С��������Ϊ![]() ��
��
(1)������![]() ��
��![]() ȷ���ĵ�
ȷ���ĵ�![]() �ں���
�ں���![]() ��ͼ���ϵĸ��ʣ�
��ͼ���ϵĸ��ʣ�
(2)С����С��Լ����һ����Ϸ�������Ϊ����![]() ��
��![]() ����
����![]() ��6��С��ʤ����
��6��С��ʤ����![]() ��
��![]() ����
����![]() ��6��С��ʤ�������Ϸ��ƽ��˵������.������ƽ����д����ƽ����Ϸ����.
��6��С��ʤ�������Ϸ��ƽ��˵������.������ƽ����д����ƽ����Ϸ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC�������������ֱ�ΪA����5��1����B����1��5����C����2��2��������ABC��ԭ��˳ʱ����ת90������A1B1C1����A1B1C1����A2B2C2����x��Գƣ�
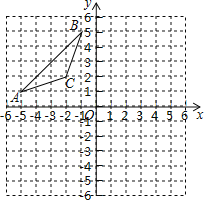
��1��������A1B1C1����A2B2C2��
��2��sin��CAB���� ����
��3����ABC����A2B2C2��ɵ�ͼ���Ƿ�����Գ�ͼ�Σ�������Գ�ͼ�Σ���ֱ��д���Գ������ڵ�ֱ�߽���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() ��
Ϊ��![]() ���е㣬������
���е㣬������![]() �Ƶ�
�Ƶ�![]() ��ת��
��ת��![]() �����߷ֱ���
�����߷ֱ���![]() ��
��![]() ����
����![]() ��
��![]() ���
���![]() ��
��![]() ��
��![]() �����غϣ�����
�����غϣ�����![]() �ֱ���
�ֱ���![]() ��
��![]() ����.
����.
��1����֤��![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�
��2����֤��![]() ��
��
��3������![]() ����̽������������
����̽������������![]() �Ƶ�
�Ƶ�![]() ��ת�Ĺ����У�
��ת�Ĺ����У�![]() ���ܳ��Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵������.
���ܳ��Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��1�����С����С������ѧ��10����ѧ���Գɼ����±�����I����ʾ��
�� | 70 | 80 | 90 | 80 | 70 | 90 | 80 | 100 | 60 | 80 |
�� | 90 | 80 | 100 | 60 | 90 | 80 | 90 | 60 | 60 | 90 |
�ָ����ϱ����ݽ���ͳ�Ƶõ��±�����������
���� | ƽ���ɼ� | ��λ�� | ���� |
�� | 80 | ||
�� | 80 | 90 |
��1����գ����ݱ�I��������ɱ�������ȱ�����ݣ�
��2����ʦ������С��ķ���![]() �������С���ķ��˵������ѧ���ijɼ���Ϊ�ȶ���
�������С���ķ��˵������ѧ���ijɼ���Ϊ�ȶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��б�߳�30cm��ֱ��������ľ�壨Rt��ACB���Ͻ�ȡһ��������CDEF����D�ڱ�BC�ϣ���E��б��AB�ϣ���F�ڱ�AC�ϣ���AF��AC��1��3�������ľ���ȡ������CDEF��ʣ�ಿ�ֵ����Ϊ________
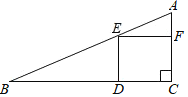
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��֪��x��Ԫ���η���x2��6x+2a+5��0����������ȵ�ʵ����x1��x2��
��1����a��ȡֵ��Χ��
��2����x12+x22��x1x2��30����aΪ��������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��![]() ��ֱ��
��ֱ��![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ��һ���㣬����
��һ���㣬����![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() �ڵ�
�ڵ�![]() ��
��![]() ������
������![]() ��
��![]() .��
.��![]() �ij�Ϊ
�ij�Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() .
.

С������ѧϰ�����ľ��飬�Ժ���![]() ���Ա���
���Ա���![]() �ı仯���仯�Ĺ��ɽ�����̽��.
�ı仯���仯�Ĺ��ɽ�����̽��.
������С����̽�����̣������С��������������.
��1��ͨ����ͼ1���о�����������㣬�õ���![]() ��
��![]() �ļ����Ӧֵ�����±���
�ļ����Ӧֵ�����±���
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 0 | 0.7 | 1.7 | 2.9 |
| 4.8 | 5.2 | 4.6 | 0 |
���������С��©�����![]() ��
��
��2����ͼ2������ƽ��ֱ������ϵ![]() ��������и���ӦֵΪ����ĵ㣬�����ú����Ĵ���ͼ��
��������и���ӦֵΪ����ĵ㣬�����ú����Ĵ���ͼ��
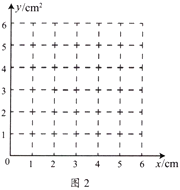
��3����ϻ����ĺ���ͼ��![]() �����Ϊ
�����Ϊ![]() ʱ�����
ʱ�����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���������˶��ᣬѧУҪ��ѧ�������ɱʴ��ͱʼDZ���Ϊ��Ʒ.����2���ʴ���1���ʼDZ��軨25Ԫ������3���ʴ���2���ʼDZ��軨40Ԫ.
��1����ʴ��ͱʼDZ��ĵ��۸��Ƕ���Ԫ?
��2��ѧУ������ʴ��ͱʼDZ�����180�����ס������̳���ͬ���۸����ͬ������Ʒ�������ָ����Ƴ���ͬ���Żݷ������ڼ��̳��ۼƹ��ﳬ��1000Ԫ����1000Ԫ�IJ��ְ�90%�շѣ������̳��ۼƹ��ﳬ��500Ԫ����500Ԫ�IJ��ְ�95%�շѣ�����Ԥ��˴ι��ﳬ����1000Ԫ����ѧУ��Ҫ���ٹ�����ٸ��ʴ�������ʹ�����̳������ʡǮ?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com