
【题目】如图1,![]() 的直径
的直径![]() ,点
,点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() ,
,![]() .设
.设![]() 的长为
的长为![]() ,
,![]() 的面积为
的面积为![]() .
.

小东根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小东的探究过程,请帮助小东完成下面的问题.
(1)通过对图1的研究、分析与计算,得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 0 | 0.7 | 1.7 | 2.9 |
| 4.8 | 5.2 | 4.6 | 0 |
请求出表中小东漏填的数![]() ;
;
(2)如图2,建立平面直角坐标系![]() ,描出表中各对应值为坐标的点,画出该函数的大致图象;
,描出表中各对应值为坐标的点,画出该函数的大致图象;
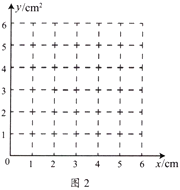
(3)结合画出的函数图象,当![]() 的面积为
的面积为![]() 时,求出
时,求出![]() 的长.
的长.
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】近年来某市大力发展绿色交通,构建公共、绿色交通体系,将“共享单车”陆续放置在人口流量较大的地方,琪琪同学随机调查了若干市民用“共享单车”的情况,将获得的数据分成四类,![]() :经常使用;
:经常使用;![]() :偶尔使用;
:偶尔使用;![]() :了解但不使用;
:了解但不使用;![]() :不了解,并绘制了如下两个不完整的统计图.请根据以上信息,解答下列问题:
:不了解,并绘制了如下两个不完整的统计图.请根据以上信息,解答下列问题:
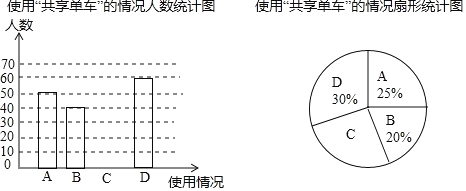
(1)这次被调查的总人数是 人,“![]() :了解但不使用”的人数是 人,“
:了解但不使用”的人数是 人,“![]() :不了解”所占扇形统计图的圆心角度数为 .
:不了解”所占扇形统计图的圆心角度数为 .
(2)某小区共有![]() 人,根据调查结果,估计使用过“共享单车”的大约有多少人?
人,根据调查结果,估计使用过“共享单车”的大约有多少人?
(3)目前“共享单车”有黄色、蓝色、绿色三种可选,某天小张和小李一起使用“共享单车”出行,求两人骑同一种颜色单车的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点![]() 、
、![]() ,以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程
,以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程![]() 与时间
与时间![]() 满足关系
满足关系![]() ,乙以
,乙以![]() 的速度匀速运动,半圆的长度为
的速度匀速运动,半圆的长度为![]() .
.
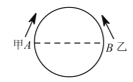
(1)甲运动![]() 后的路程是多少?
后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.

(1)本次调查的样本容量是________,这组数据的众数为________元;
(2)求这组数据的平均数;
(3)该校共有![]() 学生参与捐款,请你估计该校学生的捐款总数.
学生参与捐款,请你估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程.
已知:直线![]() 和直线外一点
和直线外一点![]() .
.
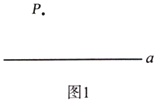
求作:直线![]() 的垂线,使它经过
的垂线,使它经过![]() .
.
作法:如图2.
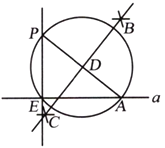
(1)在直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ;
;
(2)分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
,![]() 两点,连接
两点,连接![]() 交
交![]() 于点
于点![]() ;
;
(3)以点![]() 为圆心,
为圆心,![]() 为半径作圆,交直线
为半径作圆,交直线![]() 于点
于点![]() (异于点
(异于点![]() ),作直线
),作直线![]() .所以直线
.所以直线![]() 就是所求作的垂线.
就是所求作的垂线.
请你写出上述作垂线的依据:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
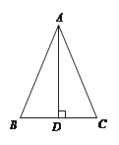
【题目】如图,△ABC中,AB=AC,过点A作AD⊥BC于点D.
(1)确定△ABC外接圆的圆心O,并画出△ABC的外接圆⊙O;(尺规作图,保留作图痕迹,不写作法)
(2)若BC=4,∠BAC=45°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.
(1)试求点E的坐标(用含m,n的式子表示);
(2)求证:AM=AN;
(3)若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种货物的数量与3月份相同,4月份共收取运费13000元.试求该物流公司3月份运输A、B两种货物各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是唐初作为“算学”教科书的著名的《算经十书》之一,共三卷,上卷叙述算筹记数的制度和乘除法则,中卷举例说明筹算分数法和开平方法,都是了解中国古代筹算的重要资料,下卷收集了一些算术难题,“鸡兔同笼”便是其中一题.下卷中还有一题,记载为:“今有甲乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八.问甲、乙二人持钱各几何?”意思是:“甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文.如果乙得到甲所有钱的![]() ,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
A.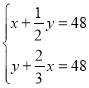 B.
B.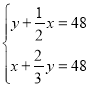 C.
C.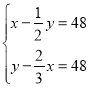 D.
D.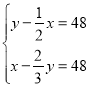
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com