
【题目】在等边△ABC中,点D为AC上一点,连接BD,直线l与AB,BD,BC分别相交于点E,P,F,且∠BPF=60°.
(1)如图(1),写出图中所有与△BPF相似的三角形,并选择其中一对给予证明;
(2)若直线l向右平移到图(2),图(3)的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不需证明),若不成立,请说明理由;
(3)探究:如图(1),当BD满足什么条件时(其它条件不变),EF=![]() BF?请写出探究结果,并说明理由.
BF?请写出探究结果,并说明理由.

【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)先判断出∠BPF=∠EBF=60°,再结合公共角即可得出结论;
(2)同(2)的方法即可得出结论;
(3)由BD平分∠ABC得到∠ABP=∠PBF=30°,再由∠BPF=60°得到∠BEP=90°,从而得到∠BEF=30°,再利用锐角三角函数tan60°=![]() 即可得出结论.
即可得出结论.
(1)△BPF∽△EBF,△BPF∽△BCD.
以△BPF∽△EBF为例,证明如下:
∵∠BPF=∠EBF=60°,∠BFP=∠BFE,
∴△BPF∽△EBF.
(2)△BPF∽△EBF,△BPF∽△BCD成立.
(3)当BD平分∠ABC时,EF=![]() BF.理由如下:
BF.理由如下:
∵BD平分∠ABC,
∴∠ABP=∠PBF=30°.
∵∠BPF=60°,
∴∠BEP=90°,
∴∠BEF=60°-30°=30°.
在Rt△BEF中,∠EBF=60°,
∴tan60°=![]() ,即EF=
,即EF=![]() BF.
BF.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
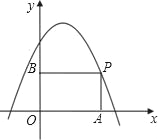
【题目】如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )
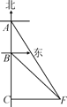
A. 10![]() 海里 B. (10
海里 B. (10![]() -10)海里
-10)海里
C. 10海里 D. (10![]() -10)海里
-10)海里
查看答案和解析>>
科目:初中数学 来源: 题型:
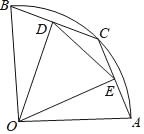
【题目】如图,在半径为1的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当![]() 时,求线段OD的长;
时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出是哪条边,并求其长度;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
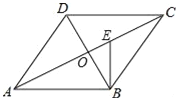
【题目】如图,在ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:AC⊥BD;
(2)若AB=14,cos∠CAB=![]() ,求线段OE的长.
,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
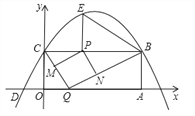
【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
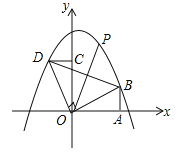
【题目】如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线![]() 经过B、D两点.
经过B、D两点.
(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个钢筋三角架三边长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( ).
A. 一种 B. 两种 C. 三种 D. 四种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com