
分析 (1)根据待定系数法即可求得;
(2)把求得的解析式化成顶点式即可得出函数的最小值,根据最小值即可证得;
(3)根据平移的规律,是顶点纵坐标等于或小于1即可.
解答 (1)解:由题意得:$\left\{\begin{array}{l}{c=3}\\{9a+3b+c=6}\\{4a-2b+c=11}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=3}\end{array}\right.$,
∴该函数的函数关系式为:y=x2-2x+3.
(2)证明:∵y=x2-2x+3=(x-1)2+2,
∴当x=1时,y取最小值2,
∴无论x取何值,函数值y总不等于1.
(3)将该函数图象向下平移的距离大于等于1个单位长度.
点评 本题考查了待定系数法求二次函数的解析式,二次函数的性质以及二次函数的图象与几何变换,熟练掌握待定系数法是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
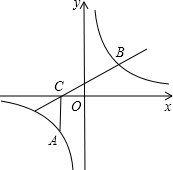 如图,点A为双曲线y=$\frac{k}{x}$(k>0)上一点,AC⊥x轴于C,过C的直线l交双曲线于B,∠BCO=30°,BC=2$\sqrt{3}$,点A横坐标为-1.
如图,点A为双曲线y=$\frac{k}{x}$(k>0)上一点,AC⊥x轴于C,过C的直线l交双曲线于B,∠BCO=30°,BC=2$\sqrt{3}$,点A横坐标为-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
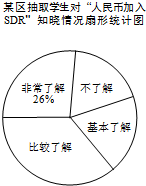 “世界那么大,我想去看看”一句话红遍网络,随着国际货币基金组织正式宣布人民币2016年10月1日加入SDR(特别提款权),以后出国看世界更加方便.为了解某区6000名初中生对“人民币加入SDR”知晓的情况,某校数学兴趣小组随机抽取区内部分初中生进行问卷调查,将问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不了解”四个等级,并将调查结果整理分析,得到下列图表:
“世界那么大,我想去看看”一句话红遍网络,随着国际货币基金组织正式宣布人民币2016年10月1日加入SDR(特别提款权),以后出国看世界更加方便.为了解某区6000名初中生对“人民币加入SDR”知晓的情况,某校数学兴趣小组随机抽取区内部分初中生进行问卷调查,将问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不了解”四个等级,并将调查结果整理分析,得到下列图表: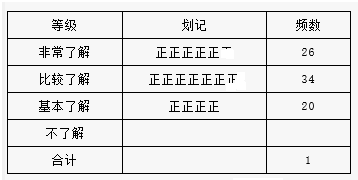
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{a}{b}}$ | C. | $\sqrt{{a}^{2}+1}$ | D. | $\sqrt{4a+4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
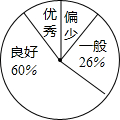 某校为了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
某校为了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:| 阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com