
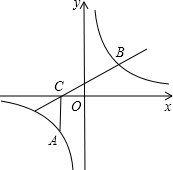
 如图,点A为双曲线y=$\frac{k}{x}$(k>0)上一点,AC⊥x轴于C,过C的直线l交双曲线于B,∠BCO=30°,BC=2$\sqrt{3}$,点A横坐标为-1.
如图,点A为双曲线y=$\frac{k}{x}$(k>0)上一点,AC⊥x轴于C,过C的直线l交双曲线于B,∠BCO=30°,BC=2$\sqrt{3}$,点A横坐标为-1.分析 (1)过点B作BD⊥x轴于点D.由“AC⊥x轴于C,点A横坐标为-1”可知C点的坐标为(-1,0),在Rt△BDC中,通过∠BCD的正余弦值可求出点B的坐标,将点B的坐标代入反比例函数中即可求出k的值;
(2)利用(1)中的k值得出反比例函数的解析式,将x=-1代入其中求出点A的坐标,结合三角形的面积公式即可得出结论.
解答 解:(1)过点B作BD⊥x轴于点D,如图1所示.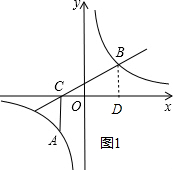
∵AC⊥x轴于C,点A横坐标为-1,
∴点C的坐标为(-1,0).
在Rt△BDC中,∠BCO=30°,BC=2$\sqrt{3}$,
∴BD=BC•sin∠BCD=$\sqrt{3}$,CD=BC•cos∠BCD=3,OD=CD-OC=2,
∴点B的坐标为(2,$\sqrt{3}$).
将点B(2,$\sqrt{3}$)代入到双曲线y=$\frac{k}{x}$中得:
$\sqrt{3}$=$\frac{k}{2}$,解得:k=2$\sqrt{3}$.
(2)依照题意画出图形,如图2所示.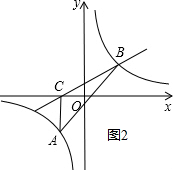
反比例函数的解析式为y=$\frac{2\sqrt{3}}{x}$.
令x=-1,则y=$\frac{2\sqrt{3}}{-1}$=-2$\sqrt{3}$,
即点A的坐标为(-1,-2$\sqrt{3}$).
S△ABC=$\frac{1}{2}$×1×[$\sqrt{3}$-(-2$\sqrt{3}$)]=$\frac{3\sqrt{3}}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及三角形的面积公式,解题的关键是:(1)求出B点的坐标;(2)由A、B点的坐标结合三角形的面积公式求出△ABC的面积.本题属于基础题,难度不大,解决该题型题目时,通过解直角三角形找出点的坐标再利用待定系数法求函数解析式是关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
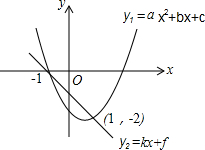 若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )
若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )| A. | $\left\{\begin{array}{l}{mx<1}\\{nx>1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{mx>1}\\{nx>1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{mx>1}\\{nx<1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{mx<1}\\{nx<1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
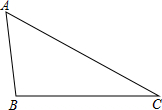 如图,在△ABC中,AB=3,BC=5,AC=6,请解答下列问题:
如图,在△ABC中,AB=3,BC=5,AC=6,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
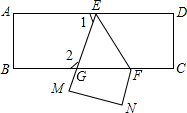 如图已知,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上.若∠EFG=55°,求∠1和∠2的度数.
如图已知,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上.若∠EFG=55°,求∠1和∠2的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com