
分析 (1)先移项,再合并同类项,把x的系数化为1即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)移项得,3x-x<2,
合并同类项得,2x<2,
把x的系数化为1得,x<1;
(2)原式=$\frac{(x+1)^{2}}{x+1}$•$\frac{x-1}{(x+1)(x-1)}$-$\frac{x}{x+2}$
=(x+1)•$\frac{1}{x+1}$-$\frac{x}{x+2}$
=1-$\frac{x}{x+2}$
=$\frac{2}{x+2}$,
当x=$\sqrt{2}$-2时,原式=$\frac{2}{\sqrt{2}-2+2}$=$\sqrt{2}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
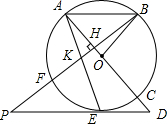 如图,AC是⊙O的直径,BF是⊙O的弦,BF⊥AC于点H,在BF上截取KB=AB,AK的
如图,AC是⊙O的直径,BF是⊙O的弦,BF⊥AC于点H,在BF上截取KB=AB,AK的查看答案和解析>>
科目:初中数学 来源: 题型:选择题
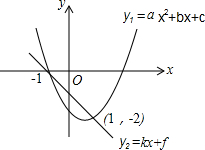 若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )
若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )| A. | $\left\{\begin{array}{l}{mx<1}\\{nx>1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{mx>1}\\{nx>1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{mx>1}\\{nx<1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{mx<1}\\{nx<1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
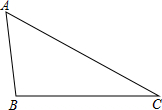 如图,在△ABC中,AB=3,BC=5,AC=6,请解答下列问题:
如图,在△ABC中,AB=3,BC=5,AC=6,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
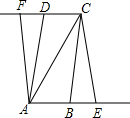 如图,?ABCD中,AB=2cm,AC=5cm,S?ABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,同时,点F从D点出发,以同样的速度在CD延长线上向左运动,运动时间为t秒.
如图,?ABCD中,AB=2cm,AC=5cm,S?ABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,同时,点F从D点出发,以同样的速度在CD延长线上向左运动,运动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com