
ЁОЬтФПЁПФГГЌЪаГЌЪазМБИЙКНјAЁЂBСНжжЦЗХЦЕФЪщАќЙВ100ИіЃЌвбжЊСНжжЪщАќЕФНјМлШчЯТБэЫљЪОЃЌЩшЙКНјAжжЪщАќxИіЃЌЧвЫљЙКНјЕФСНжжЪщАќФмШЋВПТєГіЃЌЛёЕУЕФзмРћШѓЮЊyдЊЃЎ
ЦЗХЦ | ЙКТђИіЪ§ЃЈИіЃЉ | НјМлЃЈдЊ/ИіЃЉ | ЪлМлЃЈдЊ/ИіЃЉ | ЛёРћЃЈдЊЃЉ |
A | x | 50 | 60 | __________ |
B | __________ | 40 | 55 | __________ |
ЃЈ1ЃЉНЋБэИёЕФаХЯЂЬюаДЭъећЃЛ
ЃЈ2ЃЉЧѓyЙигкxЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉШчЙћЙКНјСНжжЪщАќЕФзмЗбгУВЛГЌЙ§4500дЊЧвЙКНјBжжЪщАќЕФЪ§СПВЛДѓгкAжжЪщАќЕФ3БЖЃЌФЧУДГЌЪаШчКЮНјЛѕВХФмЛёРћзюДѓЃПВЂЧѓГізюДѓРћШѓЃЎ
ЁОД№АИЁПЃЈ1ЃЉБэИёМћНтЮіЃЛЃЈ2ЃЉy=5x+1500ЃЛЃЈ3ЃЉx=25ЃЌзюДѓРћШѓЪЧ1375дЊ.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшЙКНјAжжЪщАќxИіЃЌИљОнГЌЪазМБИЙКНјAЁЂBСНжжЦЗХЦЕФЪщАќЙВ100ИіЃЌПЩжЊЙКНјBжжЪщАќЃЈ100-xЃЉИіЃЌдйИљОнРћШѓЕШгкУПИіЪщАќЕФРћШѓЁСИіЪ§ЃЌМЦЫуМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЩшЙКНјAжжЪщАќxИіЃЌдђЙКНјBжжЪщАќЃЈ100-xЃЉИіЃЌИљОнзмРћШѓy=AжжЪщАќЕФРћШѓ+BжжЪщАќЕФРћШѓЃЌЛЏМђОЭПЩвдЕУГіНсТлЃЛ
ЃЈ3ЃЉИљОнЙКНјСНжжЪщАќЕФзмЗбгУВЛГЌЙ§4500дЊЧвЙКНјBжжЪщАќЕФЪ§СПВЛДѓгкAжжЪщАќЕФ3БЖЃЌСаГіВЛЕШЪНзщЧѓГіЦфНтЃЌИљОнИљОнвЛДЮКЏЪ§ЕФаджЪЕУГіД№АИМДПЩЃЎ
ЪдЬтНтЮіЃК
(1)ЬюБэШчЯТЃК
ЦЗХЦ | ЙКТђИіЪ§(Иі) | НјМл(дЊ/Иі) | ЪлМл(дЊ/Иі) | ЛёРћ(дЊ) |
A | x | 50 | 60 | 10x |
B | 100x | 40 | 55 | 15(100x) |
ЙЪД№АИЮЊ100xЃЛ10xЃЛ15(100x)ЃЛ
(2)y=10x+15(100x)=5x+1500ЃЌ
МДyЙигкxЕФКЏЪ§БэДяЪНЮЊy=5x+1500ЃЛ
(3)гЩЬтвтПЩЕУ![]() ЃЌ
ЃЌ
НтЕУ25ЁмxЁм50ЃЌ
Ёпy=5x+1500ЃЌ5<0ЃЌ
ЁрyЫцxЕФдіДѓЖјМѕаЁЃЌ
ЁрЕБx=25ЪБ,yгазюДѓжЕ,зюДѓжЕЮЊЃК5ЁС25+1500=1375(дЊ).
МДЕБЙКНјAжжЪщАќ25ИіЃЌBжжЪщАќ75ИіЪБЃЌГЌЪаПЩвдЛёЕУзюДѓРћШѓЃЛзюДѓРћШѓЪЧ1375дЊЁЃ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпLЩЯгаШ§Иіе§ЗНаЮaЃЌbЃЌcЃЌШєaЃЌcЕФУцЛ§ЗжБ№ЮЊ1КЭ9ЃЌдђbЕФУцЛ§ЮЊЃЈ ЃЉ
A.8
B.9
C.10
D.11
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃЈЃ2ЃЉ2009+ЃЈЃ2ЃЉ2010ЕФНсЙћЪЧЃЈ ЃЉ
A. 22019 B. 22009 C. Ѓ2 D. Ѓ22010
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЮвЙњЙХЫуЪщЁЖжмїТЫуОЁЗжаОЭгаЁАШєЙДШ§ЃЌЙЩЫФЃЌдђЯвЮхЁБЕФМЧди.ШчЭМ1ЪЧгЩБпГЄЯрЕШЕФаЁе§ЗНаЮКЭжБНЧШ§НЧаЮЙЙГЩЕФЃЌПЩвдгУЦфУцЛ§ЙиЯЕбщжЄЙДЙЩЖЈРэ.ЭМ2ЪЧгЩЭМ1ЗХШыГЄЗНаЮФкЕУЕНЕФЃЌЁЯBAC=90ЁуЃЌAB=6ЃЌAC=8ЃЌЕуDЃЌEЃЌFЃЌGЃЌHЃЌ IЖМдкГЄЗНаЮKLMJЕФБпЩЯЃЌдђГЄЗНаЮKLMJЕФУцЛ§ЮЊЃЈ ЃЉ
A.360
B.400
C.440
D.484
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЕФЖЅЕуЗжБ№ЮЊAЃЈ-2,3ЃЉЃЌBЃЈ-3,2ЃЉЃЌCЃЈ-1,1ЃЉ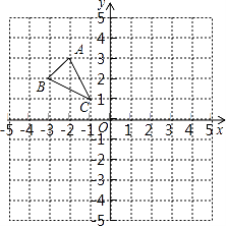 A2B2C2
A2B2C2
ЃЈ1ЃЉЛГіЁїABCЙигкyжсЖдГЦЕФЁї ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧыдкxжсЩЯШЗЖЈвЛЕуDЃЌЪЙЕуDЕНBЁЂCЕФОрРыЯрЕШЃЈвЊЧѓгУжБГпКЭдВЙцзїЭМЃЌВЂБЃСєзїЭМКлМЃЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаИїЪНМЦЫуе§ШЗЕФЪЧЃЈ ЃЉ
A.ЃЈa+bЃЉ2=a2+b2
B.aa2=a3
C.a8ЁТa2=a4
D.a2+a3=a5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпl1ЃКy=x+3гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌгыжБЯпl2ЃКy=Љ ![]() xНЛгкЕуPЃЎжБЯпl3ЃКy=Љ
xНЛгкЕуPЃЎжБЯпl3ЃКy=Љ ![]() x+4гыxжсНЛгкЕуCЃЌгыyжсНЛгкЕуDЃЌгыжБЯпl1НЛгкЕуQЃЌгыжБЯпl2НЛгкЕуRЃЎ
x+4гыxжсНЛгкЕуCЃЌгыyжсНЛгкЕуDЃЌгыжБЯпl1НЛгкЕуQЃЌгыжБЯпl2НЛгкЕуRЃЎ 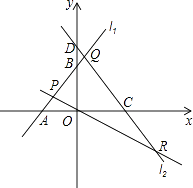
ЃЈ1ЃЉЕуAЕФзјБъЪЧ ЃЌ ЕуBЕФзјБъЪЧ ЃЌ ЕуPЕФзјБъЪЧЃЛ
ЃЈ2ЃЉНЋЁїPOBбиyжселЕўКѓЃЌЕуPЕФЖдгІЕуЮЊPЁфЃЌЪдХаЖЯЕуPЁфЪЧЗёдкжБЯпl3ЩЯЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЧѓЁїPQRЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШє 4x2ЉЃЈkЉ1ЃЉx+9 ФмгУЭъШЋЦНЗНЙЋЪНвђЪНЗжНтЃЌдђ k ЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com