
分析 (1)将所求式子的分子、分母同时除以ab,即可化成a-b=-3ab,然后把所求的分式化成利用ab表示的形式,然后化简即可求解;
(2)首先把已知的式子进行平方求得x2+$\frac{1}{{x}^{2}}$的值,然后根据(x-$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$-2计算,最后开方即可.
解答 解:(1)∵$\frac{1}{a}-\frac{1}{b}=3$,
∴$\frac{b-a}{ab}$=3,即a-b=-3ab,
则原式=$\frac{2(a-b)+3ab}{a-b}$=$\frac{-6ab+3ab}{-3ab}$=$\frac{-3ab}{-3ab}$=1;
(2)∵x+$\frac{1}{x}=6$,
∴(x+$\frac{1}{x}$)2=36,即x2+$\frac{1}{{x}^{2}}$+2=36,则x2+$\frac{1}{{x}^{2}}$=34,
∴(x-$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$-2=34-2=32,
又∵0<x<1,
∴x<$\frac{1}{x}$,
∴x-$\frac{1}{x}$=-$\sqrt{32}$=-4$\sqrt{2}$.
点评 本题考查了分式的化简求值以及完全平方公式,理解完全平方公式的变形是关键.


科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点,动点P从点A出发,沿A→B→A的方向以1cm/s的速度运动,当回到点A时停止运动,连接PD.设点P的运功时间为t(s).△BOP的面积为S(cm2)(这里规定:线段是面积为O的几何图形).
如图,在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点,动点P从点A出发,沿A→B→A的方向以1cm/s的速度运动,当回到点A时停止运动,连接PD.设点P的运功时间为t(s).△BOP的面积为S(cm2)(这里规定:线段是面积为O的几何图形).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
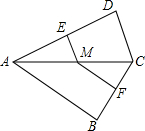 如图,四边形ABCD中,∠B=∠D=90°,M是AC上一点,ME⊥AD于点E,MF⊥BC于点F
如图,四边形ABCD中,∠B=∠D=90°,M是AC上一点,ME⊥AD于点E,MF⊥BC于点F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com