
 ��ͼ����Rt��ABC�У���ACB=90�㣬AC=3cm��BC=4cm����DΪBC���е㣬����P�ӵ�A��������A��B��A�ķ�����1cm/s���ٶ��˶������ص���Aʱֹͣ�˶�������PD�����P���˹�ʱ��Ϊt��s������BOP�����ΪS��cm2��������涨���߶������ΪO�ļ���ͼ�Σ���
��ͼ����Rt��ABC�У���ACB=90�㣬AC=3cm��BC=4cm����DΪBC���е㣬����P�ӵ�A��������A��B��A�ķ�����1cm/s���ٶ��˶������ص���Aʱֹͣ�˶�������PD�����P���˹�ʱ��Ϊt��s������BOP�����ΪS��cm2��������涨���߶������ΪO�ļ���ͼ�Σ������� ��1�����ݹ��ɶ��������������ε��ж������ʽ��н�ɣ�
��2���֢ٵ�0��t��5ʱ���ڵ�5��t��10ʱ������������н�ɣ�
��3������PD��ACʱ���������������ε��ж������ʽ�ɣ�
��4������P��PF��BC���������������ε��ж������ʽ��н��
��� �⣺��1����ͼ1������D��DE��AB������Ϊ��E��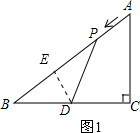
���BED=��BCA=90�㣬
��AB=$\sqrt{A{C}^{2}+B{C}^{2}}=5$��
�ߡ�B=��B��
���BDE�ס�BAC��
��$\frac{DE}{AC}=\frac{BD}{AB}$��
�ߵ�DΪBC���е㣬
��BD=$\frac{1}{2}$BC=2��
��$\frac{DE}{3}=\frac{2}{5}��DE=\frac{6}{5}$��
���D��AB�ľ���Ϊ$\frac{6}{5}$��
��2���ٵ�0��t��5ʱ��BP=5-t��
${S}_{��BDP}=\frac{1}{2}BP•DE$��
��$S=\frac{1}{2}��\frac{6}{5}��5-t��=-\frac{3}{5}t+3$��
�ڵ�5��t��10ʱ��BP=t-5��
${S}_{��BDP}=\frac{1}{2}BP•DE$��
$S=\frac{1}{2}��\frac{6}{5}��t-5��=\frac{3}{5}t-3$��
��3����ͼ2����PD��ACʱ��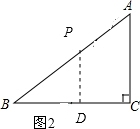
���BDP�ס�BCA��
��$\frac{PB}{AB}=\frac{BD}{BC}=\frac{1}{2}$��
��$\frac{5-t}{5}=\frac{1}{2}��\frac{t-5}{5}=\frac{1}{2}$��
��ã�t=2.5��t=7.5��
��4��t=$\frac{15}{7}$��t=$\frac{55}{7}$��
��ͼ3������P��PF��BC������Ϊ��F��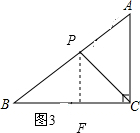
���PFB=��ACB=90�㣬
��PF��AC��
���BFP�ס�BCA��
��$\frac{PF}{AC}=\frac{BF}{BC}=\frac{BP}{BA}$��
��$\frac{PF}{3}=\frac{BF}{4}=\frac{5-t}{5}��PF=\frac{3}{5}��t-5����BF=\frac{4}{5}��t-5��$��
��CPƽ�֡�ACB��
���PCF=��FPC=45�㣬
��CF=PF=$\frac{3}{5}��5-t����CF=PF=\frac{3}{5}��t-5��$��
��$\frac{3}{5}��5-t��+\frac{4}{5}��5-t��=4��\frac{3}{5}��t-5��+\frac{4}{5}��t-5��=4$��
��$t=\frac{15}{7}��t=\frac{55}{7}$��
���� ���⿼�������������ε����ʺ��ж������ɶ���������������������������ǽ����Ĺؼ������˷�������˼�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
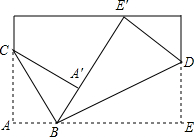 ͬѧ�ǣ��������ֽ��Ϸ����ֽ��Ϸ�ﻹ�̲��Ų�����ѧ֪ʶ��!����һ�ų�����ֽƬ������С���ķ�����ֽ���۵���A��B��E��B��ͬһֱ���ϣ���ͼ��ʾ�������ۺ�BC��BD�ļнǡ�CBD�Ķ���Ϊ90�㣮
ͬѧ�ǣ��������ֽ��Ϸ����ֽ��Ϸ�ﻹ�̲��Ų�����ѧ֪ʶ��!����һ�ų�����ֽƬ������С���ķ�����ֽ���۵���A��B��E��B��ͬһֱ���ϣ���ͼ��ʾ�������ۺ�BC��BD�ļнǡ�CBD�Ķ���Ϊ90�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�����㣺��ֱ֪��AB����һ��C��M���߶�AC���е㣬��BC=4cm��AB=10cm����AM�ij���
��ͼ�����㣺��ֱ֪��AB����һ��C��M���߶�AC���е㣬��BC=4cm��AB=10cm����AM�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��Rt��ABC�У���C=90�㣬AB=10��AC=8��E��AC��һ�㣬AE=5��ED��AB������Ϊ��D����AD�ij�Ϊ��������
��ͼ��Rt��ABC�У���C=90�㣬AB=10��AC=8��E��AC��һ�㣬AE=5��ED��AB������Ϊ��D����AD�ij�Ϊ��������| A�� | $\frac{25}{4}$ | B�� | 6 | C�� | $\frac{24}{5}$ | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
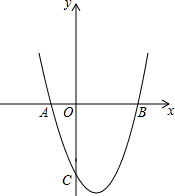 ��ͼ��������y=x2+bx+c��x�ύ��A��-1��0����B��3��0�����㣮
��ͼ��������y=x2+bx+c��x�ύ��A��-1��0����B��3��0�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com