
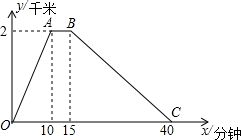
 李老师每天坚持晨跑.如图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象.其中x(分钟)表示所用时间,y(千米)表示李欢离家的距离.
李老师每天坚持晨跑.如图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象.其中x(分钟)表示所用时间,y(千米)表示李欢离家的距离.分析 (1)利用待定系数法即可求得;
(2)求出OA的解析式,然后根据OA、BC的解析式,利用y=0.5千米计算求出相应的x的值,再加上6点20分即可.
解答 解:(1)设OA的解析式为y1=kx,
则10k=2,
解得k=$\frac{1}{5}$,
所以,y=$\frac{1}{5}$x,
设直线BC解析式为y2=k1x+b,
∵函数图象经过点(15,2),(40,0),
∴$\left\{\begin{array}{l}{15{k}_{1}+b=2}\\{40{k}_{1}+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=-\frac{2}{25}}\\{b=\frac{16}{5}}\end{array}\right.$.
所以,直线BC解析式为y=-$\frac{2}{25}$x+$\frac{16}{5}$;
∴线段0≤x≤10的函数解析式为y1=$\frac{1}{5}$x(0≤x≤10),
线段15≤x≤40的函数解析式为y2=-$\frac{2}{25}$x+$\frac{16}{5}$(15≤x≤40);
(2)当y1=0.5km时,0.5=$\frac{1}{5}$x,x=2.5
当y2=0.5km时,0.5=-$\frac{2}{25}$x+$\frac{16}{5}$,x=$\frac{135}{4}$=33.75,
∴李老师在这次晨跑过程中分别于6点22.5分和6点53.75分距离家500米.
点评 本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,已知函数值求自变量,准确识图,理解转折点的坐标的意义是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
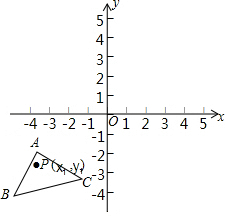 如图,已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
如图,已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 锐角三角形的三条高线、三条中线、三条角平分线分别交于一点 | |
| B. | 钝角三角形有两条高线在三角形外部 | |
| C. | 直角三角形只有一条高线 | |
| D. | 任意三角形都有三条高线、三条中线、三条角平分线 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
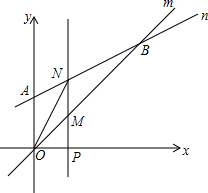 如图,在平面直角坐标系中,直线m:y=kx过原点,直线n:y=$\frac{1}{2}$x+4与y轴交于点A,与直线m交于点B(8,8),x轴上一点P(t,0)从原点出发沿x轴向右运动,过点P作直线PM⊥x轴,分别交直线m,n与点M,N,连接ON.
如图,在平面直角坐标系中,直线m:y=kx过原点,直线n:y=$\frac{1}{2}$x+4与y轴交于点A,与直线m交于点B(8,8),x轴上一点P(t,0)从原点出发沿x轴向右运动,过点P作直线PM⊥x轴,分别交直线m,n与点M,N,连接ON.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
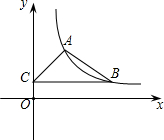 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$ (x>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$ (x>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com