
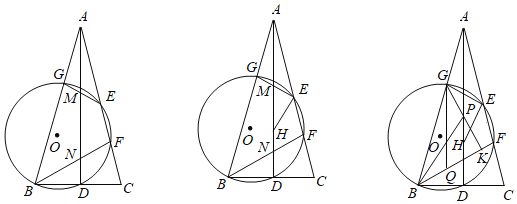
����Ŀ����ͼ����ABC�У�AB��AC��AD��BC��D��E��AC����һ�㣬��O��B��D��E���㣬�ֱ�AC��AB�ڵ�F��G������EG��BF�ֱ���AD���ڵ�M��N��
��1����֤����AMG����BND��
��2������EΪAC���е㣬��֤��BF��BC��
��3���ڣ�2���������£���EH��EG��AD�ڵ�H����EH��EG��4![]() ������G��GK��BF�ڵ�K����P���߶�GK�ϣ���Q���߶�BK�ϣ�����BP��GQ������KGQ��2��GBP��GQ��15
������G��GK��BF�ڵ�K����P���߶�GK�ϣ���Q���߶�BK�ϣ�����BP��GQ������KGQ��2��GBP��GQ��15![]() ����GP�ij��ȣ�
����GP�ij��ȣ�
���𰸡���1������������2������������3��![]()
��������
��1������Բ�ڽ��ı��ε����ʺͲ��ǵ����ʿ�֤��BFE����AGE���ٸ����������ڽǺͶ�����֤��AMG����ANF�������ɵý��ۣ�
��2������DE����֤��BD��CD���ɵ���FBC����BAC��֤����BFC����ABC����C�����۵�֤��
��3��ȡAB�е�P������MH��GH��DE���ɵ�ƽ���ı���BDEM���ȱ���MHE���ɵó���GAH����GHA��15�������GA��GH��![]() EH��
EH��![]() �����AE��
�����AE��![]() �������AB��BG����Rt��BGK�У��ɵ���GBK��45�������GK��BK��
�������AB��BG����Rt��BGK�У��ɵ���GBK��45�������GK��BK��![]() ��Rt��QGK�й��ɶ����ɵ�QK��
��Rt��QGK�й��ɶ����ɵ�QK��![]() ���ӳ�BK��TʹKT��PK������GK����BKP�ա�GKT���ó���KGT����KBP���ɵ�QG��QT��15
���ӳ�BK��TʹKT��PK������GK����BKP�ա�GKT���ó���KGT����KBP���ɵ�QG��QT��15![]() ����PK�������GP��GK��PK��
����PK�������GP��GK��PK��![]() ��
��
��1��֤������AB��AC��AD��BC��
���BAD����CAD��
���ı���BFEG�ڽ�����O��
���BGE+��BFE��180��
�ߡ�BGE+��AGE��180����
���BFE����AGE��
�ߡ�AGM�У���BAD+��AGE+��AMG��180����
��ANF����CAD+��BFE+��ANF��180����
���AMG����ANF��
�ߡ�ANF����BND��
���AMG����BND��
��2��֤������ͼ������DE��
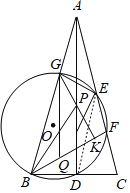
��AB��AC��AD��BC��
��BD��CD��
��AE��CE��
��DE����ABC����λ�ߣ�
��DE��AB��
���DEC����BAC��
�ߡ�DEC����FBC��
���FBC����BAC��
�ߡ�C=��C��
���ABC�ס�BFC��
���ABC=��BFC��
��AB��AC��
���ABC����C��
���BFC����ABC����C��
��BF��BC��
��3���⣺��ͼ��ȡAB�е�M������MH��ME��DE��
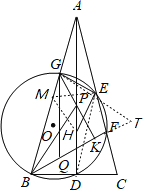
��AE��CE��AM=BM��
��ME�ǡ�ABC����λ�ߣ�
��ME��BD��
���GME����ABC��
�ߡ�ABC����C����C����EDC����BGE��
���MGE����GME��
��GE��ME��
��MH��ME��EH��EG��
���MHE�ǵȱ������Σ�
��AD��ֱƽ��BC��
��AH��ֱƽ��ME��
���GAH����GHA��15����
![]() EH��
EH��![]() ��
��![]() ��
��
������AGE��AE��![]() ��
��
��AB��AC��![]() ��
��
��BG��AB��AG��![]() ��
��
��Rt��BGK�У��ɵ���GBK��45����
��GK��BK��![]() ��
��
��Rt��QGK��QK��![]() ��
��![]() ��
��
�ӳ�BK��TʹKT��PK������GK��
�ߡ�BKP����GKT��
���BKP�ա�GKT��SAS����
���KGT����KBP�����BPK����GTK��
�ߡ�QGT����KGQ+��KGT����KGQ+��PBK��
��KGQ��2��GBP��
���QGT��2��GBP+��PBK��
�ߡ�PBK��45������GBP��
���QGT��45��+��PBG����BPK��
���QGT����GTK��
��QG��QT��15![]() ��
��
��PK��KT��QT��QK��![]() ��
��
��GP��GK��PK��12![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ƻ�����A��B���ֲ�Ʒ��100������֪A��Ʒÿ���ɻ�����400Ԫ��B��Ʒÿ���ɻ�����500Ԫ�����й涨����B��Ʒ������������A��Ʒ������2����������A��Ʒ������Ϊx(��)���������ֲ�Ʒ�Ļ����ܶ�Ϊy(Ԫ)
��1��д��y��x֮��ĺ�������ʽ��
��2���ó�����A��B���ֲ�Ʒ������̨������ʹ�����ܶ������������Ƕ��٣�
��3����ʵ�����������У�A��Ʒ�����ɱ��½���m(0��m��200)Ԫ���������60����B��Ʒ�����ɱ����䣬�����������Ϣ����Ƴ��ó�����100��A��B���ֲ�Ʒ������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��b��cΪ��������x�ύ�ڵ�
��b��cΪ��������x�ύ�ڵ�![]() ��
��![]() ����y�ύ�ڵ�A����EΪ�����߶��㡣
����y�ύ�ڵ�A����EΪ�����߶��㡣
����![]() ʱ�����A����E�����ꣻ
ʱ�����A����E�����ꣻ
����������E��ֱ��![]() �ϣ�����Aλ�����ʱ���������ߵĽ���ʽ��
�ϣ�����Aλ�����ʱ���������ߵĽ���ʽ��
������![]() ����
����![]() ����
����![]() ֵ��Сʱ����b��ֵ��
ֵ��Сʱ����b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
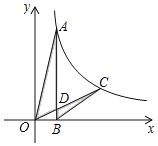
����Ŀ����ͼ����֪��A����C�ڷ���������y��![]() ��k��0��x��0����ͼ���ϣ�AB��x���ڵ�B��OC��AB�ڵ�D����CD��OD������AOD����BCD�������Ϊ__��
��k��0��x��0����ͼ���ϣ�AB��x���ڵ�B��OC��AB�ڵ�D����CD��OD������AOD����BCD�������Ϊ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������EFG�У���EFG��90����EF��FG���ҵ�E��F�ֱ��ھ���ABCD�ı�AB��AD�ϣ�
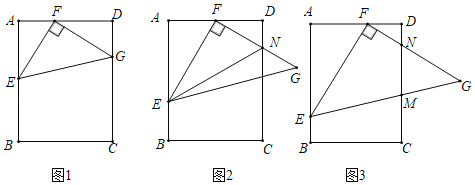
��1����ͼ1������G��CD��ʱ����֤����AEF�ա�DFG��
��2����ͼ2����F��AD���е㣬FG��CD�ཻ�ڵ�N������EN����֤��EN��AE+DN��
��3����ͼ3����AE��AD��EG��FG�ֱ�CD�ڵ�M��N����֤��MG2��MNMD.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ʻ��������Ҫ�����������Ƚ�ͨ����ʵʩ��ijУ��ѧ����ʵ��С��Ͷ���Щ��ͨ������˽������ȫУ��������˲���ѧ������������Ϊ���֣�A���dz��˽⣬B���Ƚ��˽⣬C�������˽⣬D����̫�˽⣬ʵ��С��Ѵ˴ε��������������Ƴ����治����������ͳ��ͼ������ͳ��ͼ��
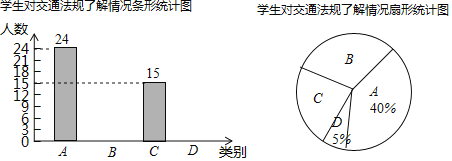
����ͼ��������Ϣ����������⣺
��1�����ι�����������ѧ��������ͳ��ͼ��C����Ӧ���ε�Բ�ĽǶ�����������
��2����ȫ����ͳ��ͼ��
��3����У����800��ѧ��������������Ϣ���������ȫУѧ���ж���Щ��ͨ�������dz��˽������ж�������
��4��ͨ���˴ε��飬��ѧ����ʵ��С���ѧ���Խ�ͨ�������˸������ʶ��ѧУ�������ڵļס��ҡ���������λѧ���������ȡ����ѧ���μ�������ͨ���澺���������б�����״ͼ�ķ������������ѧ��ͬʱ��ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2��bx��c(a��0)�IJ���ͼ���䶥������Ϊ(1��n)����������x���һ�������ڵ�(3��0)��(4��0)֮�䣮�����н���

��a��b��c��0����3a��b��0��
��b2��4a(c��n)��
��һԪ���η���ax2��bx��c��n��1����������ȵ�ʵ������
������ȷ���۵ĸ�����(����)
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ҵ�н����Ϻ����������Ʒ������ҵ�����ǹ��ù����170cm��40cm�ı������Ϊԭ���ϣ�ÿ�ű�����ٰ��ղ÷�һ��÷�������A����B�����ְ�ģ���ͼ1��ʾ������λ��cm��
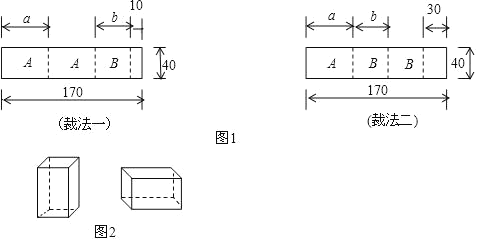
��1���г����̣��飩�����ͼ����a��b��ֵ��
��2������30�ű�����ò÷�һ�ü���4�ű�����ò÷����ü����ٽ��õ���A����B�Ͱ��������͵��棬����ͼ2����ʽ���ʽ��������Ʒ�У�
�����ֲ÷�������A�Ͱ���� ���ţ�B�Ͱ���� ���ţ�
�����ɵ���ʽ�ͺ�ʽ��������Ʒ����������Ƕ��ٸ�����ʱ��ʽ����Ʒ�п��������ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����֪����AOCD��ƽ��ֱ������ϵxOy�У���CAO��60����OA��2��B�������Ϊ��2��0��������M��ÿ��2����λ���ȵ��ٶ���A��C��B�˶���M�㲻���A����B�غϣ������˶�ʱ��Ϊt�룮
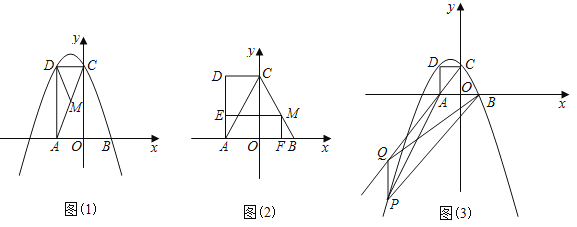
��1����B��C��D����������߽���ʽ��
��2����P�ڣ�1���е��������ϣ���MΪAC�е�ʱ������PAM�ա�PDM�����P�����ꣻ
��3������M��CB���˶�ʱ����ͼ��2������M��ME��AD��MF��x�ᣬ����ֱ�ΪE��F�������AEMF����ABC�ص��������ΪS����S��t�ĺ�����ϵʽ�������S�����ֵ��
��4����ͼ��3����P�ڣ�1���е��������ϣ�Q��CA�ӳ����ϵ�һ�㣬��P��Q������ڵ��������ڣ�Q��A��λ��ֱ��BPͬ��IJ�ͬ���㣬����P��x��ľ���Ϊd����QPB�����Ϊ2d�����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com