
【题目】如图(1)已知矩形AOCD在平面直角坐标系xOy中,∠CAO=60°,OA=2,B点的坐标为(2,0),动点M以每秒2个单位长度的速度沿A→C→B运动(M点不与点A、点B重合),设运动时间为t秒.
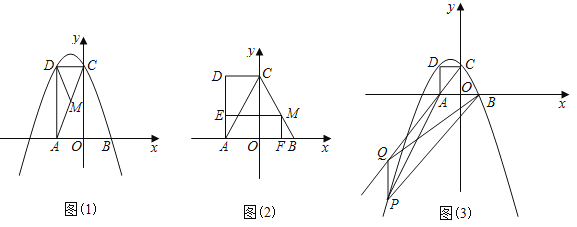
(1)求经过B、C、D三点的抛物线解析式;
(2)点P在(1)中的抛物线上,当M为AC中点时,若△PAM≌△PDM,求点P的坐标;
(3)当点M在CB上运动时,如图(2)过点M作ME⊥AD,MF⊥x轴,垂足分别为E、F,设矩形AEMF与△ABC重叠部分面积为S,求S与t的函数关系式,并求出S的最大值;
(4)如图(3)点P在(1)中的抛物线上,Q是CA延长线上的一点,且P、Q两点均在第三象限内,Q、A是位于直线BP同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2d,求点P的坐标.
【答案】(1)y= ![]() ;(2)点P(﹣1+
;(2)点P(﹣1+![]() ,
,![]() )或(﹣1﹣
)或(﹣1﹣![]() ,
,![]() );(3)S=﹣
);(3)S=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,当t=
,当t=![]() 时,S最大=
时,S最大=![]() ;(4)P(﹣8,-10
;(4)P(﹣8,-10![]() )
)
【解析】
(1)由直角三角形的性质可求点C,点D坐标,由待定系数法可求解析式;
(2)由全等三角形的性质可得DM=AM,PD=AP,可得点P在AD的垂直平分线上,可求点P的纵坐标,代入可求解;
(3)由题意可证△ACB是等边三角形,可得CM=2t-4,BF=![]() (8﹣2t)=4﹣t,MF=4
(8﹣2t)=4﹣t,MF=4![]() ﹣
﹣![]() t,AF=t,即可求重叠部分面积,由二次函数的性质可求解;
t,AF=t,即可求重叠部分面积,由二次函数的性质可求解;
(4)由题意先求出直线AC,BP的解析式,即可求点P坐标.
解:(1)∵四边形ABCD是矩形,
∴CD=AO=2,∠AOC=90°,且∠CAO=60°,OA=2,
∴OC=2![]() ,
,
∴点C(0,2![]() ),点D(﹣2,2
),点D(﹣2,2![]() ),
),
设抛物线解析式为y=a(x+1)2+c,代B(2,0),C(0,2![]() )
)
∴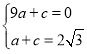
解得: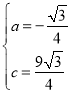
∴抛物线解析式为y=﹣![]() (x+1)2+
(x+1)2+![]() =
=![]() ,
,
(2)∵M为AC中点,
∴MA=MD,
∵△PAM≌△PDM,
∴PA=PD,
∴点P在AD的垂直平分线上
∴点P纵坐标为![]() ,
,
∴![]()
∴x1=﹣1+![]() ,x2=﹣1﹣
,x2=﹣1﹣![]()
∴点P(﹣1+![]() ,
,![]() )或(﹣1﹣
)或(﹣1﹣![]() ,
,![]() )
)
(3)如图2,
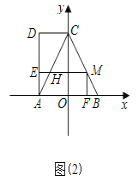
∵AO=BO=2,CO⊥AB,
∴AC=BC=4,∠CAO=60°,
∴△ACB是等边三角形,
由题意可得:CM=2t﹣4,BF=![]() (8﹣2t)=4﹣t,MF=4
(8﹣2t)=4﹣t,MF=4![]() ﹣
﹣![]() t,AF=t.
t,AF=t.
∵四边形AEMF是矩形,
∴AE=MF,EM=AF,EM∥AB,
∴∠CMH=∠CBA=60°,∠CHM=∠CAO=60°,
∴△CMH是等边三角形,
∴CM=MH=2t﹣4,
∵S=![]() (2t﹣4+t)(4
(2t﹣4+t)(4![]() ﹣t)=﹣
﹣t)=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]()
当t=![]() 时,S最大=
时,S最大=![]() ,
,
(4)∵S△ABP=![]() ×4×d=2d,
×4×d=2d,
又S△BPQ=2d
∴S△ABP=S△BPQ,
∴AQ∥BP
设直线AC解析式为y=kx+b,
把A(﹣2,0),C(0,2![]() )代入其中,得
)代入其中,得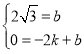
∴
∴直线AC解析式为:y=![]() x+2
x+2![]() ,
,
设直线BP 的解析式为y=![]() x+n,把B(2,0)代入其中,得
x+n,把B(2,0)代入其中,得
0=2![]() +n,
+n,
∴b=﹣2![]()
∴直线BP解析式为:y=![]() x﹣2
x﹣2![]() ,
,
∴![]() =
=![]() x﹣2
x﹣2![]() ,
,
∴x1=2(舍去),x2=﹣8,
∴P(﹣8,-10![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
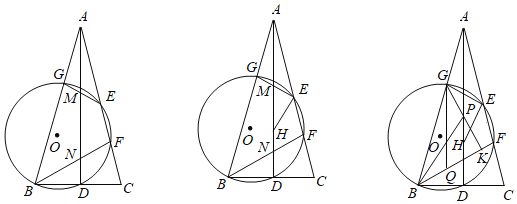
【题目】如图,△ABC中,AB=AC,AD⊥BC于D,E是AC边上一点,⊙O过B、D、E三点,分别交AC、AB于点F、G,连接EG、BF分别与AD交于点M、N;
(1)求证:∠AMG=∠BND;
(2)若点E为AC的中点,求证:BF=BC;
(3)在(2)的条件下,作EH⊥EG交AD于点H,若EH=EG=4![]() ,过点G作GK⊥BF于点K,点P在线段GK上,点Q在线段BK上,连接BP、GQ,若∠KGQ=2∠GBP,GQ=15
,过点G作GK⊥BF于点K,点P在线段GK上,点Q在线段BK上,连接BP、GQ,若∠KGQ=2∠GBP,GQ=15![]() ,求GP的长度.
,求GP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
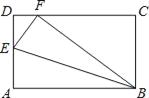
【题目】已知:如图,矩形ABCD中,AB=5,BC=3,E为AD上一点,把矩形ABCD沿BE折叠,若点A恰好落在CD上点F处,则AE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.
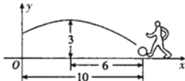
(1)如图建立直角坐标系,当球飞行的路线为一抛物线时,求此抛物线的解析式.
(2)已知球门高为2.44米,问此球能否射中球门(不计其它情况).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(m+1)x﹣m﹣2(m>0)与x轴交于A、B两点,与y轴交于点C,不论m取何正数,经过A、B、C三点的⊙P恒过y轴上的一个定点,则该定点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
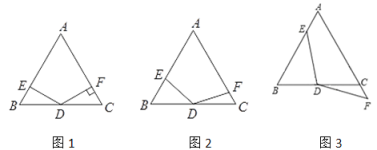
(1)如图1,若DF⊥AC,垂足为F,证明:DE=DF
(2)如图2,将∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.DE=DF仍然成立吗?说明理由.
(3)如图3,将∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线相交于点F,DE=DF仍然成立吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的不断提高,龙岗区家庭轿车的拥有量逐年增加.据统计,某小区2017年底拥有家庭轿车81辆,2019年底家庭轿车的拥有量达到144辆.
(1)若该小区2017年底到2019年底家庭轿车拥有量的年平均增长率都相同,求该小区到2020年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资25万元再建造若干个停车位.据测算,建造费用分别为室内车位6000元/个,露天车位2000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的3倍,但不超过室内车位的4.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△DEF中,EF=10,DF=6,DE=8,以EF的中点O为圆心,作半圆与DE相切,点A、B分别是半圆和边DF上的动点,连接AB,则AB的最大值与最小值的和是( )

A.6B.2![]() +1C.
+1C.![]() D.9
D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com