
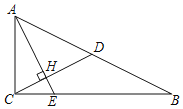
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sin∠CAH的值;
(2)如果CD=![]() ,求BE的值.
,求BE的值.
【答案】(1)![]() ;(2)3
;(2)3
【解析】
(1)由勾股定理得出AC=![]() =
=![]() CH,由锐角三角函数定义即可得出答案;
CH,由锐角三角函数定义即可得出答案;
(2)根据sinB的值,可得出AC:AB=1:![]() ,由AB=2
,由AB=2 ![]() ,得AC=2,设CE=x(x>0),则AE=
,得AC=2,设CE=x(x>0),则AE=![]() x,由勾股定理得出方程,求出CE=1,从而得出BE.
x,由勾股定理得出方程,求出CE=1,从而得出BE.
解:(1)∵AE⊥CD,
∴∠AHC=90°,
∵AH=2CH,
∴由勾股定理得:AC=![]() =
=![]() CH,
CH,
∴sin∠CAH=![]() ;
;
(2)∵∠ACB=90°,CD是斜边AB上的中线,
∴AB=2CD=2 ![]() ,
,
∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,
又∵∠ACB=90°,
∴∠BCD+∠ACH=90°,
∴∠B=∠BCD=∠CAH,
∵sinB=![]() =sin∠CAH=
=sin∠CAH=![]() =
=![]() ,
,
∴AC:AB=1:![]() ,
,
∴AC=2.
设CE=x(x>0),则AE=![]() x,
x,
在Rt△ACE中,由勾股定理得:x2+22=(![]() x)2,
x)2,
解得:x=1,
∴CE=1,
在Rt△ABC中,由勾股定理得:BC=![]() =
=![]() =4,
=4,
∴BE=BC﹣CE=3.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.

(1)请你用直尺和圆规补全这个输水管道的圆形截面(保留作图痕迹);
(2)若这个输水管道有水部分的水面宽AB=24cm,水面最深地方的高度为8cm,求这个圆形截面的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=﹣![]() x2+x﹣4,下列说法正确的是( )
x2+x﹣4,下列说法正确的是( )
A.图象的开口方向向上
B.当x>0 时,y随x的增大而增大
C.当x=2时,y有最大值﹣3
D.图象与x轴有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,二次函数![]() (
(![]() )图象的顶点为
)图象的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 点右侧),点
点右侧),点![]() ,
,![]() 关于直线
关于直线![]() 对称.
对称.
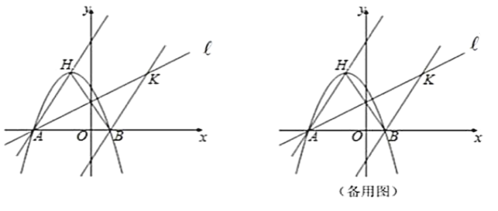
(1)![]() 坐标为 ;
坐标为 ;![]() 坐标为: ;
坐标为: ;![]() 坐标为 ;
坐标为 ;
(2)求二次函数解析式;
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 最大?若不存在,请说明理由:若存在,请求出此时
最大?若不存在,请说明理由:若存在,请求出此时![]() 的面积;
的面积;
(4)过点![]() 作直线
作直线![]() 交直线
交直线![]() 于
于![]() 点,
点,![]() ,
,![]() 分别为直线
分别为直线![]() 和直线
和直线![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 和的最小值.
和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
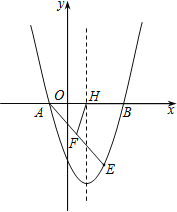
【题目】如图,抛物线y=x2+bx+c经过点A(﹣1,0),B(3,0).请解答下列问题:
(1)求抛物线的解析式;
(2)点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.
注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 上部分点的横坐标x与纵坐标y的对应值如下表
上部分点的横坐标x与纵坐标y的对应值如下表
x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | -4 | 0 | 2 | 2 | 0 | -4 | … |
下列结论:①抛物线开口向下;②当![]() 时,y随x的增大而减小;③抛物线的对称轴是直线
时,y随x的增大而减小;③抛物线的对称轴是直线![]() ;④函数
;④函数![]() 的最大值为2.其中所有正确的结论为( )
的最大值为2.其中所有正确的结论为( )
A.①②③B.①③C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
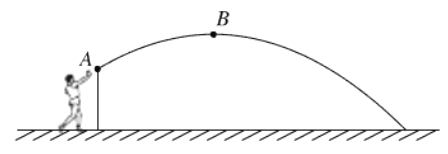
【题目】为了在校运会中取得更好的成绩,小丁积极训练.在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是![]() 米,当铅球运行的水平距离为3米时,达到最大高度
米,当铅球运行的水平距离为3米时,达到最大高度![]() 的B处.小丁此次投掷的成绩是多少米?
的B处.小丁此次投掷的成绩是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
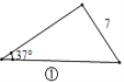
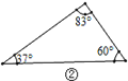
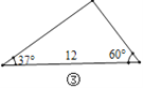
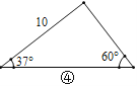
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是____.
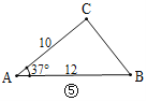
(2)如图⑤,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:
,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售一批名牌衬衫,平均每天可售出40件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件.
(1)若商场平均每天要盈利2400元,每件衬衫应降价多少元?
(2)若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com