
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.

(1)请你用直尺和圆规补全这个输水管道的圆形截面(保留作图痕迹);
(2)若这个输水管道有水部分的水面宽AB=24cm,水面最深地方的高度为8cm,求这个圆形截面的半径.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,l1、l2、l3两两相交于A、B、C三点,它们与y轴正半轴分别交于点D、E、F,若A、B、C三点的坐标分别为(1,yA)、(2,yB)、(3,yC),且OD=DE=1,则下列结论正确的个数是( )①EC=3EA,②S△ABC=1,③OF=5,④2yA﹣yA﹣yC=2
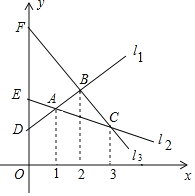
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,P是AC上的一点,PH⊥AB于点H,以PH为直径作⊙O,当CH与PB的交点落在⊙O上时,AP的值为( )
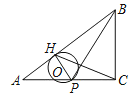
A.![]() B.
B.![]() C.2D.3
C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,线段AB的端点坐标分别为A(0,6)、B(6,6).点Q在线段AB上,以Q为项点的抛物线y=﹣![]() x2+bx+c与y轴交于点D,与x轴的一个交点为C.设点Q的横坐标为m,点C的横坐标为n(n>m).
x2+bx+c与y轴交于点D,与x轴的一个交点为C.设点Q的横坐标为m,点C的横坐标为n(n>m).
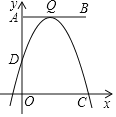
(1)当m=0时,求n的值.
(2)求线段AD的长(用含m的式子表示);
(3)点P(2,0)在x轴上,设△BPD的面积为S,求S与m的关系式;
(4)当△DCQ是以QC为直角边的直角三角形时,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长是6,∠A=60°,E是AD的中点,F是AB边上一个动点,EG=EF且∠GEF=60°,则GB+GC的最小值是_____
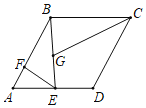
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年,国家卫生健康委员会和国家教育部在全国开展了儿童青少年近视调查工作,调查数据显示,全国儿童青少年近视过半.某校初三学习小组为了解本校学生对自己视力保护的重视程度,随机在校内调查了部分学生,调查结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成下面的两幅不完整的统计图:
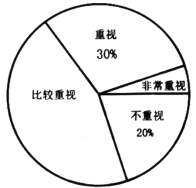
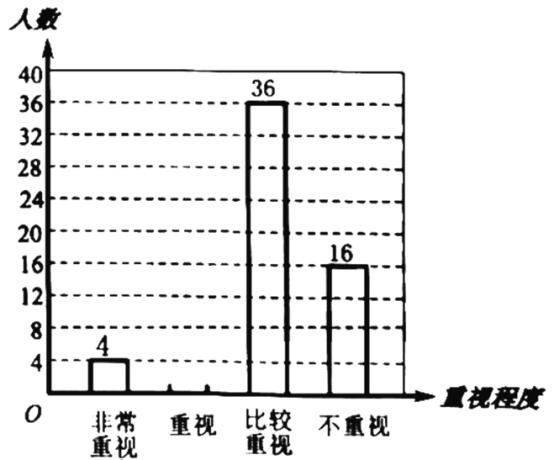
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)该校共有学生1000人,请你估计该校对视力保护“非常重视”的学生人数;
(3)对视力“非常重视”的4人有![]() ,
,![]() 两名男生,
两名男生,![]() ,
,![]() 两名女生,若从中随机抽取两人向全校作视力保护交流,请利用树状图或列表的方法,求恰好抽到一男一女的概率.
两名女生,若从中随机抽取两人向全校作视力保护交流,请利用树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
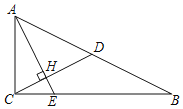
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sin∠CAH的值;
(2)如果CD=![]() ,求BE的值.
,求BE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com