
【题目】 计算:
(1)2x3(-x)2-(-x2)2(-3x);
(2)(2x-5)(3x+2);
(3)![]() ;
;
(4)用乘法公式简便计算:2002-400×199+1992
【答案】(1)5x5;(2)6x2-11x-10;(3)-11;(4)1
【解析】
(1)先算幂的乘方、再算单项式乘单项式、最后合并同类项即可求解;
(2)根据多项式乘多项式的计算法则进行计算即可求解;
(3)先算平方、零指数幂、负整数指数幂,再算加减法即可求解;
(4)利用完全平方公式计算即可求出值.
解:(1)2x3(-x)2-(-x2)2(-3x)
=2x3x2-x4(-3x);
=2x5+3x5
=5x5;
(2)(2x-5)(3x+2)
=6x2+4x-15x-10
=6x2-11x-10;
(3)![]()
=-1+1-9-2
=-11;
(4)2002-400×199+1992
=(200-199)2
=12
=1.


科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中放有四张卡片,每张卡片上写有一个实数,分别为2,![]() ,
,![]() ,1.(卡片除了实数不同外,其余均相同)
,1.(卡片除了实数不同外,其余均相同)
(1)从盒子中随机抽取一张卡片,请直接写出卡片上的实数是有理数的概率;
(2)将卡片揺匀后先随机抽出一张,再从剩下的卡片中随机抽出一张,然后将抽取的两张卡片上的实数相乘,请你用列表法或树状图(树形图)法,求抽取的两张卡片上的实数之积为整数的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
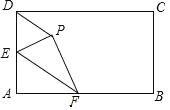
【题目】如图,在矩形ABCD中,AB=8,AD=4,点E、F分别在线段AD、AB上,将△AEF沿EF翻折,使得点A落在矩形ABCD内部的P点,连接PD,当△PDE是等边三角形时,BF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知港口A东偏南10°方向有一处小岛B,一艘货轮从港口A沿南偏东40°航线出发,行驶80海里到达C处,此时观测小岛B在北偏东60°方向.
(1)求此时货轮到小岛B的距离.
(2)在小岛周围36海里范围内是暗礁区,此时轮船向正东方向航行有没有触礁危险?请作出判断并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小蚂蚁在9×9的小方格上沿着网格线运动(每小格边长为1),一只蚂蚁在C处找到食物后,要通知A、B、D、E处的其他小蚂蚁,我们把它的行动规定:向上或向右为正,向下或向左为负。如果从C到D记为:C→D(+2,-3)(第一个数表示左、右方向,第二个数表示上、下方向),那么;

(1)C→B( ),C→E( ),D→ (-4,-3),D→ ( ,+3);
(2)若这只小蚂蚁的行走路线为C→E→D→B→A→C,请你计算小蚂蚁走过的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 推理填空
已知:如图所示,点B,C,E在同一条直线上,AB∥CD,∠1=∠2,∠3=∠4,求证:AD∥BE
证明:∵AB∥CD(已知)
∴∠4=∠______(______)
∵∠3=∠4(已知)∴∠3=∠______(______)
∴∠1=∠2(已知)∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠DAC
∴∠3=∠______(等量代换)
∴AD∥BE(______)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)若∠ABE=15°,∠BAD=40°,则∠BED=________°;
(2)请在图中作出△BED中BD边上的高EF;
(3)若△ABC的面积为40,BD=5,则点E到BC边的距离为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com