
【题目】关于x的方程ax2﹣(3a+1)x+2(a+1)=0有两个不相等的实根x1、x2,且有x1﹣x1x2+x2=1﹣a,则a的值是( )
A. 1B. ﹣1C. 1或﹣1D. 2
【答案】B
【解析】
由关于x的方程有两个不相等的实数根,得到根的判别式的值大于0列出关于a的不等式,求出不等式的解集得到a的范围,再利用根与系数的关系表示出两根之和与两根之积,代入已知的等式中得到关于a的方程,求出方程的解即可得到a的值.
解:依题意△>0,即(3a+1)2﹣8a(a+1)>0,
即a2﹣2a+1>0,(a﹣1)2>0,a≠1,
∵关于x的方程ax2﹣(3a+1)x+2(a+1)=0有两个不相等的实根x1、x2,且有x1﹣x1x2+x2=1﹣a,
∴x1﹣x1x2+x2=1﹣a,
∴x1+x2﹣x1x2=1﹣a,
∴![]() =1﹣a,
=1﹣a,
解得:a=±1,又a≠1,
∴a=﹣1.
故选:B.


科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
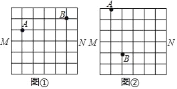
【题目】图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,点A、B、M、N均落在格点上,在图①、图②给定的网格中按要求作图.
(1)在图①中的格线MN上确定一点P,使PA与PB的长度之和最小
(2)在图②中的格线MN上确定一点Q,使∠AQM=∠BQM.
要求:只用无刻度的直尺,保留作图痕迹,不要求写出作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的实验最有可能的是( )

A. 袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球
B. 掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数
C. 先后两次掷一枚质地均匀的硬币,两次都出现反面
D. 先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9
查看答案和解析>>
科目:初中数学 来源: 题型:
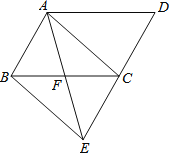
【题目】如图,在![]() 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
(1)求证:AB=CE;
(2)若![]() ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
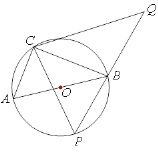
【题目】如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为![]() ,
,![]() ,则CQ的最大值是____________.
,则CQ的最大值是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=mx﹣1交y轴于点B,交x轴于点C,以BC为边的正方形ABCD的顶点A(﹣1,a)在双曲线y=﹣![]() (x<0)上,D点在双曲线y=
(x<0)上,D点在双曲线y=![]() (x>0)上,则k的值为( )
(x>0)上,则k的值为( )
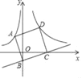
A. 6 B. 5 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
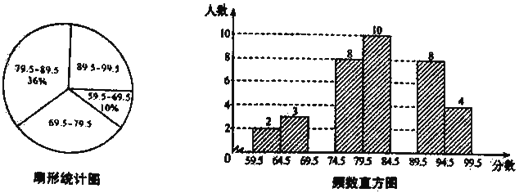
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
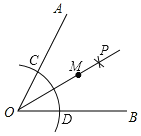
【题目】如图所示,∠AOB=70°,以点O为圆心,以适当长为半径作弧分别交OA,OB于C,D两点;分别以C,D为圆心,以大于![]() CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com