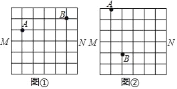
【题目】图①、图②均是8×8的正方形网格，每个小正方形的顶点称为格点，点A、B、M、N均落在格点上，在图①、图②给定的网格中按要求作图．
（1）在图①中的格线MN上确定一点P，使PA与PB的长度之和最小
（2）在图②中的格线MN上确定一点Q，使∠AQM＝∠BQM．
要求：只用无刻度的直尺，保留作图痕迹，不要求写出作法．
备战中考寒假系列答案科目：初中数学 来源： 题型：
【题目】如图，抛物线y＝ax2+bx+c的对称轴是x＝
，小亮通过观察得出了下面四个结论：①c＜0，②a﹣b+c＞0，③2a﹣3b＝0，④5b﹣2c＜0．其中正确的有（ ）
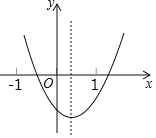
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
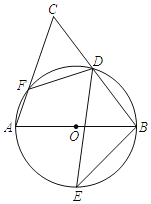
【题目】如图，AB是⊙O的直径，D，E为⊙O上位于AB异侧的两点，连结BD并延长至点C，使得CD＝BD，连结AC交⊙O于点F，连接BE，DE，DF．
（1）若∠E＝35°，求∠BDF的度数．
（2）若DF＝4，cos∠CFD＝
，E是
的中点，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A(﹣3，y1)，B(2，y2)均在抛物线y＝ax2+bx+c上，点P(m，n)是该抛物线的顶点，若y1＞y2≥n，则m的取值范围是( )
A.﹣3＜m＜2B.﹣
＜m＜-
C.m＞﹣D.m＞2
查看答案和解析>>
科目：初中数学 来源： 题型：
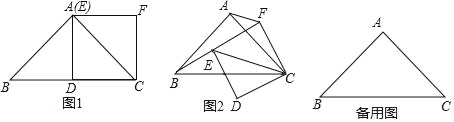
【题目】(1)（问题发现）如图1，在Rt△ABC中，AB＝AC，∠BAC＝90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，请判断线段BE与AF的数量关系并写出推断过程；
(2)（拓展研究）在(1)的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；
(3)（结论运用）在(1)(2)的条件下，若△ABC的面积为2，当正方形CDEF旋转到B，E，F三点在同一直线上时，请直接写出线段AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
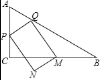
【题目】如阁，在△ABC中，∠ACB＝90°，AC＝3，BC＝4，点P从点A出发，沿折线AC﹣BC以每秒1个单位长度的速度向终点B运动，当点P不与点A、B重合时，在边AB上取一点Q，满足∠PQA＝2∠B，过点Q作QM⊥PQ，交边BC于点M，以PQ、QM为边作矩形PQMN，设点P的运动时间为t秒
（1）用含t的代数式表示线段PQ的长；
（2）当矩形PQMN为正方形时，求t的值；
（3）设矩形PQMN与△ABC重叠部分图形的周长为l，求l与t之间的函数关系式；
（4）作点A关于直线PQ的对称点A′，作点C关于直线PN的对称点C′，当点A′、C′这两个点中只有一个点在矩形PQMN内部时，直接写出此时的t取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
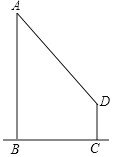
【题目】如图，一位同学想利用树影测量树高（AB），他在某一时刻测得高为1m的竹竿影长为0.9m，但当他马上测量树影时，因树靠近一幢建筑物，影子不全落在地面上，有一部分影子在墙上（CD），他先测得留在墙上的影高（CD）为1.2m，又测得地面部分的影长（BC）为2.7m，他测得的树高应为多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】关于x的方程ax2﹣（3a+1）x+2（a+1）＝0有两个不相等的实根x1、x2，且有x1﹣x1x2+x2＝1﹣a，则a的值是（ ）
A. 1B. ﹣1C. 1或﹣1D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】秋季新学期开学时，红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试，测试成绩全部合格，现学校随机选取了部分学生的成绩，整理并制作成了如下不完整的图表：
分 数 段 | 频数 | 频率 |
60≤x＜70 | 9 | a |
70≤x＜80 | 36 | 0.4 |
80≤x＜90 | 27 | b |
90≤x≤100 | c | 0.2 |
请根据上述统计图表，解答下列问题：
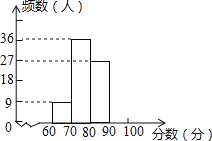
（1）在表中，a= ，b= ，c= ；
（2）补全频数直方图；
（3）根据以上选取的数据，计算七年级学生的平均成绩．
（4）如果测试成绩不低于80分者为“优秀”等次，请你估计全校七年级的800名学生中，“优秀”等次的学生约有多少人？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
