【题目】如图，在
中，点F是边BC的中点，连接AF并延长交DC的延长线于点E，连接AC、BE.
（1）求证：AB=CE；
（2）若
，则四边形ABEC是什么特殊四边形？请说明理由.
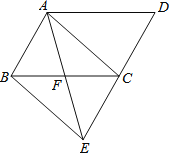
【答案】（1）证明见解析；（2）矩形，理由见解析.
【解析】
（1）根据AB//CD可知∠ABF=∠ECF，由BF=CF，∠AFB=∠CFE， 可证明△ABF≌△ECF.即可证明AB=CE.（2）根据∠AFC=2∠D 及外角性质可证明AF=BF进而证明AE=BC，即可证明四边形ABEC是平行四边形.
（1）∵F是BC的中点，
∴BF=CF.
∵在四边形
中，AB//CD，
∴∠ABF=∠ECF，
∵∠AFB=∠CFE，
∴△ABF≌△ECF，
∴AB=CE.
（2）四边形ABEC是矩形，理由如下：
∵△ABF≌△ECF，
∴EF=AF，
∵BF=CF，
∴四边形ABEC是平行四边形.
∴∠ABF=∠D，
∵∠AFC=2∠D，∠AFC=∠ABF+∠BAF，
∴∠ABF=∠BAF，
∴AF=BF，
∴AE=BC，
∴四边形ABEC是矩形．
手拉手全优练考卷系列答案科目：初中数学 来源： 题型：
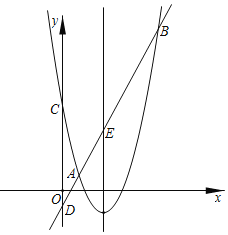
【题目】如图，抛物线y=ax2+bx+5(a≠0)交直线y=kx+n(k＞0)于A(1，1)，B两点，交y轴于点C，直线AB交y轴于点D．已知该抛物线的对称轴为直线x=
．
(1)求a，b的值；
(2)记直线AB与抛物线的对称轴的交点为E，连接CE，CB．若△CEB的面积为
，求k，n的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
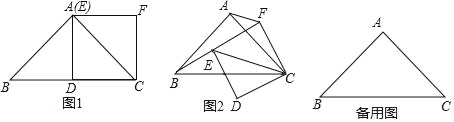
【题目】(1)（问题发现）如图1，在Rt△ABC中，AB＝AC，∠BAC＝90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，请判断线段BE与AF的数量关系并写出推断过程；
(2)（拓展研究）在(1)的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；
(3)（结论运用）在(1)(2)的条件下，若△ABC的面积为2，当正方形CDEF旋转到B，E，F三点在同一直线上时，请直接写出线段AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
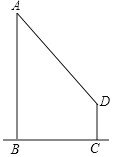
【题目】如图，一位同学想利用树影测量树高（AB），他在某一时刻测得高为1m的竹竿影长为0.9m，但当他马上测量树影时，因树靠近一幢建筑物，影子不全落在地面上，有一部分影子在墙上（CD），他先测得留在墙上的影高（CD）为1.2m，又测得地面部分的影长（BC）为2.7m，他测得的树高应为多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xoy中，A（﹣3，0），B（0，1），形状相同的抛物线Cn（n=1，2，3，4，…）的顶点在直线AB上，其对称轴与x轴的交点的横坐标依次为2，3，5，8，13，…，根据上述规律，抛物线C2的顶点坐标为_____；抛物线C8的顶点坐标为_____．
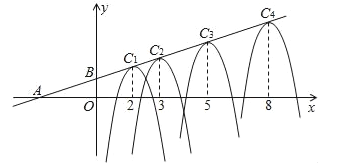
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】关于x的方程ax2﹣（3a+1）x+2（a+1）＝0有两个不相等的实根x1、x2，且有x1﹣x1x2+x2＝1﹣a，则a的值是（ ）
A. 1B. ﹣1C. 1或﹣1D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在⊙O的内接三角形ABC中，
，
，过C作AB的垂线l交⊙O于另一点D，垂足为E.设P是
上异于A，C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB于点G.
（1）求证：
；
（2）若
, 
,求PD的长.
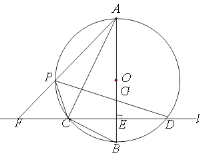
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，四边形AOBC是矩形，点O（0，0），点A（5，0），点B（0，3）．以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F．
（1）如图①，当点D落在BC边上时，求点D的坐标；
（2）如图②，当点D落在线段BE上时，AD与BC交于点H．
①求证△ADB≌△AOB；
②求点H的坐标．
（3）记K为矩形AOBC对角线的交点，S为△KDE的面积，求S的取值范围（直接写出结果即可）．
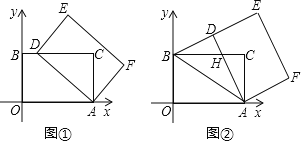
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在边长为6的正方形ABCD中，点E是射线BC上的动点（不与B，C重合），连结AE，将△ABE沿AE向右翻折得△AFE，连结CF和DF，若△DFC为等腰三角形，则BE的长为_____．
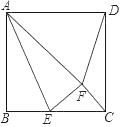
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com