
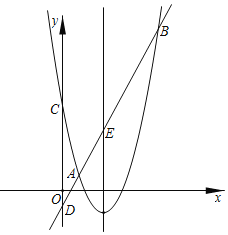
【题目】如图,抛物线y=ax2+bx+5(a≠0)交直线y=kx+n(k>0)于A(1,1),B两点,交y轴于点C,直线AB交y轴于点D.已知该抛物线的对称轴为直线x=![]() .
.
(1)求a,b的值;
(2)记直线AB与抛物线的对称轴的交点为E,连接CE,CB.若△CEB的面积为![]() ,求k,n的值.
,求k,n的值.
【答案】(1)a的值为1,b的值为–5;(2)k的值为2,n的值为–1.
【解析】
(1)根据抛物线y=ax2+bx+5(a≠0)过A(1,1),对称轴为直线x=![]() ,列出关于a、b的方程组,解方程组即可求出a,b的值;
,列出关于a、b的方程组,解方程组即可求出a,b的值;
(2)设点B(m,m25m+5),过A作AG⊥y轴于G,过B作BF⊥x轴于F,延长GA交BF于H.由DG∥BF,得出![]() =
=![]() ,求出DG=m4,那么CD=m.根据S△CEB=S△CDBS△CDE,列出方程
,求出DG=m4,那么CD=m.根据S△CEB=S△CDBS△CDE,列出方程![]() m2–
m2–![]() m×
m×![]() =
=![]() ,求出m.再把A、B两点的坐标代入y=kx+n,即可求出k,n的值.
,求出m.再把A、B两点的坐标代入y=kx+n,即可求出k,n的值.
解:(1)由题意,得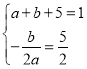 ,解得
,解得![]() ,
,
故所求a的值为1,b的值为–5;
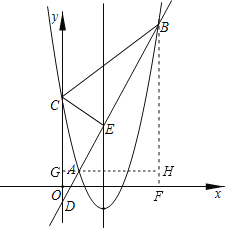
(2)由(1)可得y=x2–5x+5.可得C(0,5).
如图,设点B(m,m2–5m+5),
过A作AG⊥y轴于G,过B作BF⊥x轴于F,延长GA交BF于H.
∵DG∥BF,∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴DG=m–4,∴CD=m.
∵S△CEB=S△CDB–S△CDE,
∴![]() m2–
m2–![]() m×
m×![]() =
=![]() ,
,
解得m1=–![]() (舍去),m2=6.
(舍去),m2=6.
把A(1,1),B(6,11)代入y=kx+n,
得![]() ,解得
,解得![]() .
.
故所求k的值为2,n的值为–1.


科目:初中数学 来源: 题型:
【题目】如图,过点P作PA,PB,分别与以OA为半径的半圆切于A,B,延长AO交切线PB于点C,交半圆与于点D.
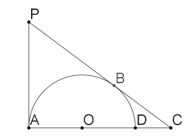
(1)若PC=5,AC=4,求BC的长;
(2)设DC:AD=1:2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
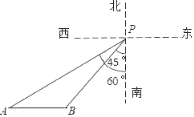
【题目】在某海域,一艘海监船在P处检测到南偏西45°方向的B处有一艘不明船只,正沿正西方向航行,海监船立即沿南偏西60°方向以40海里/小时的速度去截获不明船只,经过1.5小时,刚好在A处截获不明船只,求不明船只的航行速度.(![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留一位小数).
≈1.73,结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
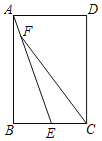
【题目】如图,在矩形ABCD中,点E是BC上一点,连接AE,点F是AE上一点,连接FC,若∠BAE=∠EFC,CF=CD,AB:BC=3:2,AF=4,则FC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
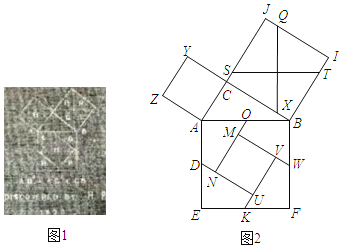
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣.英国佩里加(H.Perigal,1801﹣1898)用“水车翼轮法”(图1)证明了勾股定理.该证法是用线段QX,ST,将正方形BIJC分割成四个全等的四边形,再将这四个四边形和正方形ACYZ拼成大正方形AEFB(图2).若AD=![]() ,tan∠AON=
,tan∠AON=![]() ,则正方形MNUV的周长为( )
,则正方形MNUV的周长为( )
A. ![]() B. 18C. 16D.
B. 18C. 16D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
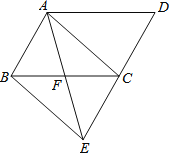
【题目】如图,在![]() 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
(1)求证:AB=CE;
(2)若![]() ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com