
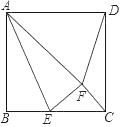
【题目】在边长为6的正方形ABCD中,点E是射线BC上的动点(不与B,C重合),连结AE,将△ABE沿AE向右翻折得△AFE,连结CF和DF,若△DFC为等腰三角形,则BE的长为_____.
【答案】2![]() 或12+6
或12+6![]() 或12﹣6
或12﹣6![]()
【解析】
分三种情形画出图形 分别求解即可.
如图,①点F在以A为圆心AB为半径的圆上,满足条件的点F在线段CD的垂直平分线KF上.
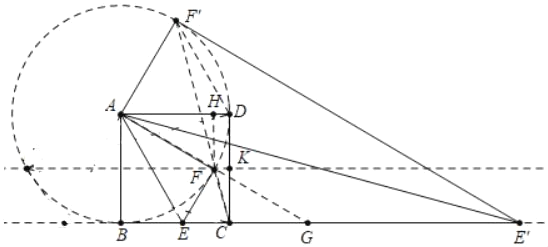
作FH⊥AD于H.在Rt△AFH中,∵AF=2FH,
∴∠FAH=30°,
∵∠BAD=90°,
∴∠BAF=60°,
∴∠EAB=∠EAF=30°,
在Rt△ABE中,BE=ABtan30°=2![]() ,
,
②当DF′=DC时,在BE′上取一点G,使得AG=GE′.
∵AF′=AD=DF′,
∴△ADF′是等边三角形,
∴∠DAF′=60°,
∴∠BAF′=150°,
∴∠BE′F′=30°,
∴∠BE′A=15°,
∵GA=GE′,
∴∠GAE′=∠GE′A=15°,
∴∠AGB=30°,
∴AG=GE′=2AB=12,BG=6![]() ,
,
∴BE′=12+6![]()
若以点D为圆心,DC长为半径作圆与以点A为圆心,AB长为半径的圆在正方形的内的交点为F
同理可得BE=12﹣6![]()
综上所述,BE的长为2![]() 或12+6
或12+6![]() 或12﹣6
或12﹣6![]()


科目:初中数学 来源: 题型:
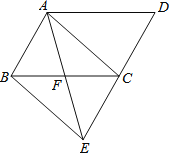
【题目】如图,在![]() 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
(1)求证:AB=CE;
(2)若![]() ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD=∠ABC,补充一个条件,使得△ABD≌△ABC,则下列选项不符合题意的是( )
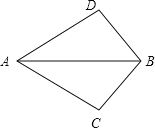
A. ∠D=∠CB. ∠DAB=∠CABC. BD=BCD. AD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为![]() ,对角线AC和BD交于点E,点F是BC边上一动点(不与点B,C重合),过点E作EF的垂线交CD于点G,连接FG交EC于点H.设BF=x,CH=y,则y与x的函数关系的图象大致是( )
,对角线AC和BD交于点E,点F是BC边上一动点(不与点B,C重合),过点E作EF的垂线交CD于点G,连接FG交EC于点H.设BF=x,CH=y,则y与x的函数关系的图象大致是( )
A. 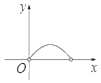 B.
B. 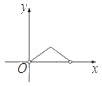 C.
C. 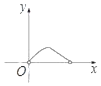 D.
D. 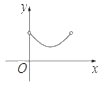
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠AOB=70°,以点O为圆心,以适当长为半径作弧分别交OA,OB于C,D两点;分别以C,D为圆心,以大于![]() CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
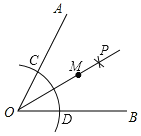
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
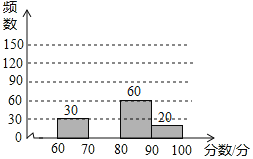
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组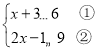 .请结合题意填空,完成本题的解答
.请结合题意填空,完成本题的解答
(Ⅰ)解不等式①,得__________;
(Ⅱ)解不等式②,得__________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
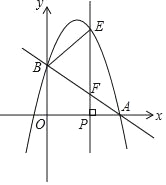
【题目】如图,在平面直角坐标系中,直线y=-![]() x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
(1)点A的坐标为 .
(2)求这条抛物线所对应的函数表达式.
(3)点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值.
(4)若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共谐点”.直接写出E、F、P三点成为“共谐点”时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com