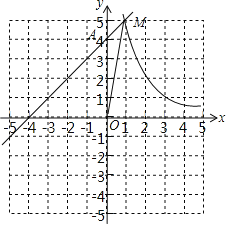
【题目】在平面直角坐标系xOy中，一次函数y＝x+4的图象与y轴交于点A，与反比例函数y＝
的图象的一个交点为M．
（1）求点A的坐标；
（2）连接OM，如果△MOA的面积等于2，求k的值．
【答案】（1）A（0，4）；（2）5或﹣3
【解析】
（1）通过计算自变量为0对应的一次函数值得到A点坐标；
（2）利用一次函数图象上点的坐标特征，设M点的坐标为（t，t+4），根据三角形面积公式得到
×4×|t|＝2，求出t得到M点的坐标，然后利用反比例函数图象上点的坐标特征求k的值．
解：（1）当x＝0，y＝x+4＝4，
∴A（0，4）；
（2）设M点的坐标为（t，t+4），
∵△MOA的面积等于2，
∴×4×|t|＝2，解得t＝1或t＝﹣1，
∴M点的坐标为（1，5）或（﹣1，3），
当M点的坐标为（1，5）时，k＝1×5＝5；
当M点的坐标为（﹣1，3）时，k＝﹣1×3＝﹣3，
综上所述，k的值为5或﹣3．
黄冈冠军课课练系列答案科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，直线x=3与直线y=
x+1交于点A，函数y=
（k＞0，x＞0）的图象与直线x=3，直线y=x+1分别交于点B，C．
（1）求点A的坐标．
（2）横、纵坐标都是整数的点叫做整点．记函数y=（k＞0，x＞0）的图象在点B，C之间的部分与线段AB，AC围成的区域（不含边界）为W．
①当k=1时，结合函数图象，求区域W内整点的个数；
②若区域W内恰有1个整点，直接写出k的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，抛物线y＝mx2﹣6mx+9m+1（m≠0）．
（1）求抛物线的顶点坐标；
（2）若抛物线与x轴的两个交点分别为A和B点（点A在点B的左侧），且AB＝4，求m的值．
（3）已知四个点C（2，2）、D（2，0）、E（5，﹣2）、F（5，6），若抛物线与线段CD和线段EF都没有公共点，请直接写出m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】ABCD中，对角线AC、BD相交于点O，E是边AB上的一个动点（不与A、B重合），连接EO并延长，交CD于点F，连接AF，CE，下列四个结论中：
①对于动点E，四边形AECF始终是平行四边形；
②若∠ABC＜90°，则至少存在一个点E，使得四边形AECF是矩形；
③若AB＞AD，则至少存在一个点E，使得四边形AECF是菱形；
④若∠BAC＝45°，则至少存在一个点E，使得四边形AECF是正方形．
以上所有正确说法的序号是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知抛物线y＝ax2+bx﹣1交y轴于点P．
（1）过点P作与x轴平行的直线，交抛物线于点Q，PQ＝4，求
的值；
（2）横纵坐标都是整数的点叫做整点．在（1）的条件下，记抛物线与x轴所围成的封闭区域（不含边界）为W．若区域W内恰有4个整点，结合函数图象，求a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝ax2﹣2ax．
（1）二次函数图象的对称轴是直线x＝ ；
（2）当0≤x≤3时，y的最大值与最小值的差为4，求该二次函数的表达式；
（3）若a＜0，对于二次函数图象上的两点P（x1，y1），Q（x2，y2），当t≤x1≤t+1，x2≥3时，均满足y1≥y2，请结合函数图象，直接写出t的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先进制造业城市发展指数是反映一个城市先进制造水平的综合指数．对2019年我国先进制造业城市发展指数得分排名位居前列的30个城市的有关数据进行收集、整理、描述和分析．下面给出了部分信息：
a．先进制造业城市发展指数得分的频数分布直方图(数据分成6组：
）：
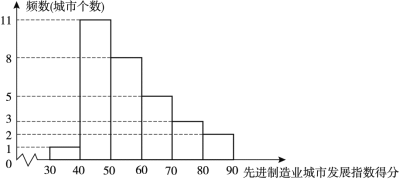
b．先进制造业城市发展指数得分在
这一组的是：71.1 75.7 79.9
c．30个城市的2019年快递业务量累计和先进制造业城市发展指数得分情况统计图：
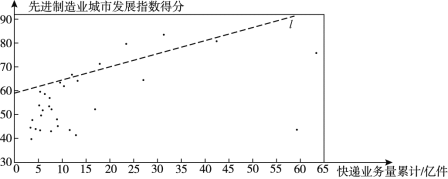
d．北京的先进制造业城市发展指数得分为79.9．
根据以上信息，回答下列问题：
（1）在这30个城市中，北京的先进制造业城市发展指数排名第
；
（2）在30个城市的快递业务量累计和先进制造业城市发展指数得分情况统计图中，包括北京在内的少数几个城市所对应的点位于虚线
的上方．请在图中用“○”圈出代表北京的点；
（3）在这30个城市中，先进制造业城市发展指数得分高于北京的城市的快递业务量累计的最小值约为_______亿件．（结果保留整数）
查看答案和解析>>
科目：初中数学 来源： 题型：
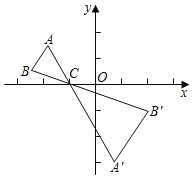
【题目】如图，△ABC中，A，B两个顶点在x轴上方，点C的坐标是(﹣1，0)，以点C为位似中心，在x轴的下方作△ABC的位似图形，并把△ABC的边长放大到原来的2倍，得到△A'B'C'，设点B的对应点B'的横坐标为2，则点B的横坐标为( )
A.﹣1B.
C.﹣2D.
查看答案和解析>>
科目：初中数学 来源： 题型：
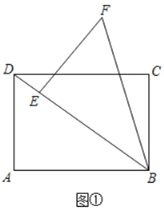
【题目】（操作）BD是矩形ABCD的对角线，AB=4，BC=3．将△BAD绕着点B顺时针旋转α度（0°＜α＜360°）得到△BEF，点A、D的对应点分别为E、F．若点E落在BD上，如图①，则DE=______．
（探究）当点E落在线段DF上时，CD与BE交于点G．其它条件不变，如图②．
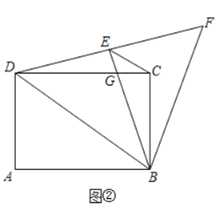
（1）求证：△ADB≌△EDB；
（2）CG的长为______．
（拓展）连结CF，在△BAD的旋转过程中，设△CEF的面积为S，直接写出S的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com