
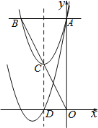
【题目】如图,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与过点
,与过点![]() 平行于
平行于![]() 轴的直线相交于点
轴的直线相交于点![]() (点
(点![]() 在第二象限),抛物线的顶点
在第二象限),抛物线的顶点![]() 在直线
在直线![]() 上,且点
上,且点![]() 为
为![]() 的中点,对称轴与
的中点,对称轴与![]() 轴相交于点
轴相交于点![]() ,平移抛物线,使其经过点
,平移抛物线,使其经过点![]() 、
、![]() ,则平移后的抛物线的解析式为________.
,则平移后的抛物线的解析式为________.
【答案】![]()
【解析】
先确定A(0,8),则表示出B点坐标(-b,8)(b>0),利用点C为OB的中点可得到C(-![]() b,4),根据抛物线的顶点坐标公式得到
b,4),根据抛物线的顶点坐标公式得到![]() =4,解得b=4或b=-4(舍去),所以抛物线解析式为y=x2+4x+8=(x+2)2+4,则D(-2,0),然后设平移后的抛物线解析式为y=x2+mx+n,再把A点和D点坐标代入得到m、n的方程组,接着解方程组求出m、n即可.
=4,解得b=4或b=-4(舍去),所以抛物线解析式为y=x2+4x+8=(x+2)2+4,则D(-2,0),然后设平移后的抛物线解析式为y=x2+mx+n,再把A点和D点坐标代入得到m、n的方程组,接着解方程组求出m、n即可.
解:当x=0时,y=x2+bx+8=8,则A(0,8),
∵AB∥x轴,
∴B点的纵坐标为8,
当y=8时,x2+bx+8=8,解得x1=0,x2=-b,
∴B(-b,8)(b>0),
∵点C为OB的中点,
∴C(-![]() b,4),
b,4),
∵C点为抛物线的顶点,
∴![]() =4,解得b=4或b=-4(舍去),
=4,解得b=4或b=-4(舍去),
∴抛物线解析式为y=x2+4x+8=(x+2)2+4,
∴抛物线的对称轴为直线x=-2,
∴D(-2,0),
设平移后的抛物线解析式为y=x2+mx+n,
把A(0,8),D(-2,0)代入得,
![]() ,解得
,解得![]() ,
,
所以平移后的抛物线解析式为y=x2+6x+8.
故答案为y=x2+6x+8.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
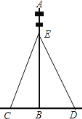
【题目】如图,为了使电线杆稳固的垂直于地面,两侧常用拉紧的钢丝绳索固定,由于钢丝绳的交点![]() 在电线杆的上三分之一处,所以知道
在电线杆的上三分之一处,所以知道![]() 的高度就可以知道电线杆
的高度就可以知道电线杆![]() 的高度了.要想得到
的高度了.要想得到![]() 的高度,需要测量出一些数据,然后通过计算得出.
的高度,需要测量出一些数据,然后通过计算得出.
请你设计出要测量的对象:________;
请你写出计算![]() 高度的思路:________.
高度的思路:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1),Q (x2,y2)的对称中心的坐标为![]() ,如图.
,如图.
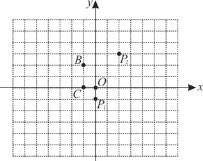
(1)在平面直角坐标系中,若点P1(0,-1),P2(2,3)的对称中心是点A,则点A的坐标为________;
(2)另取两点![]() ,
,![]() .有一电子青蛙从点P1处开始依次作关于点A,B,C的循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…,则点
.有一电子青蛙从点P1处开始依次作关于点A,B,C的循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般成年人的脚长(厘米)与鞋码(码)有如下关系:
脚长 | 23 | 23.5 | 24 | 24.5 | … |
鞋码 | 36 | 37 | 38 | 39 | … |
(1)若某人的脚长为26厘米,他应穿多少码的鞋?
(2)请建立鞋码![]() (厘米)与脚长
(厘米)与脚长![]() (码)之间的函数表达式;
(码)之间的函数表达式;
(3)我国著名篮球运动员姚明穿53码的鞋,请你根据以上关系计算他的脚长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB.
小明的做法如下:
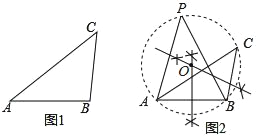
如图
①作线段AB的垂直平分线m;
②作线段BC的垂直平分线n,与直线m交于点O;
③以点O为圆心,OA为半径作△ABC的外接圆;
④在弧ACB上取一点P,连结AP,BP.
所以∠APB=∠ACB.
老师说:“小明的作法正确.”
请回答:
(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是_____;
(2)∠APB=∠ACB的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A(0,4),B(﹣3,0)反比例函数y=![]() (k为常数,k≠0,x>0)的图象经过点D.
(k为常数,k≠0,x>0)的图象经过点D.
(1)填空:k=_____.
(2)已知在y=![]() 的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com