
【题目】已知下列命题:①已知菱形的两条对角线长分别是a、b,则这个菱形的面积为![]() ab;②在Rt△ABC中,∠C=90°,若∠A>∠B,则cosA<cosB;③若m=n+1,则1﹣m2+2mn﹣n2=0;④若点A(x1,y1)和点B(x2,y2)在二次函数y=x2﹣2x﹣1的图象上,且满足x1>x2>1,则y2>y1>﹣2;其中假命题的个数是( )
ab;②在Rt△ABC中,∠C=90°,若∠A>∠B,则cosA<cosB;③若m=n+1,则1﹣m2+2mn﹣n2=0;④若点A(x1,y1)和点B(x2,y2)在二次函数y=x2﹣2x﹣1的图象上,且满足x1>x2>1,则y2>y1>﹣2;其中假命题的个数是( )
A.1B.2C.3D.4
科目:初中数学 来源: 题型:
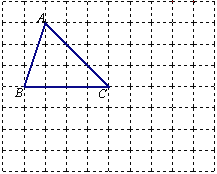
【题目】(本题满分9分)如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC.(注:顶点在网格线交点处的三角形叫做格点三角形)
(1)图中AC边上的高为_________个单位长度;
(2)只用没有刻度的直尺,按如下要求画图:
①以点C为位似中心,作△DEC∽△ABC,且相似比为1∶2;
②以AB为一边,作矩形ABMN,使得它的面积恰好为△ABC的面积的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区群众对绿化建设的满意程度,对小区内居民进行了随机调查,居民在“非常满意、满意、一般和不满意“中必选且只能选一个,并将调查结果整理后绘制成如图所示的不完整的统计图.请你根据图中提供的信息回答下列问题:
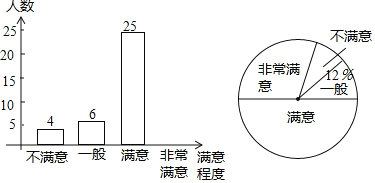
(1)本次调查共抽取了多少名居民?
(2)通过计算补全条形统计图;
(3)若该小区一共有1350人,估计该小区居民对绿化建设“非常满意”的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作EC⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.
(1)求证:AC平分∠FAB;
(2)求证:BC2=CECP;
(3)当AB=4![]() 且
且![]() =
=![]() 时,求劣弧
时,求劣弧![]() 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
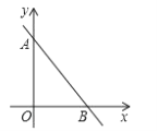
【题目】如图,在直角坐标系xOy中,O为坐标原点,直线AB分别与y轴,x轴交于A(0,4),B(3,0)两点.
(1)尺规作图:在x轴上求作一点C,使得△ABC是以![]() 为顶角的等腰三角形,并在图中标明相应字母;(保留作图痕迹,不写作法)
为顶角的等腰三角形,并在图中标明相应字母;(保留作图痕迹,不写作法)
(2)在(1)的条件下,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
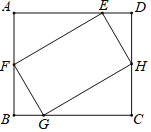
【题目】如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=![]() ;④矩形EFGH的面积是4
;④矩形EFGH的面积是4![]() .其中一定成立的是______.(把所有正确结论的序号填在横线上)
.其中一定成立的是______.(把所有正确结论的序号填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
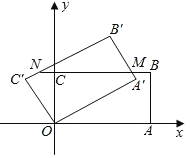
【题目】如图,平面直角坐标系中,矩形OABC绕原点O逆时针旋转30°后得到矩形OA′B′C′,A′B′与BC交于点M,延长BC交B′C′于N,若A(![]() ,0),C(0,1),则点N的坐标为( )
,0),C(0,1),则点N的坐标为( )
A.(![]() ,1)B.(
,1)B.(![]() ,1)C.(
,1)C.(![]() ,1)D.(
,1)D.(![]() ,1)
,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
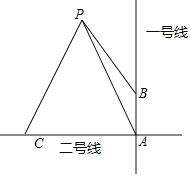
【题目】合肥地铁一号线与地铁二号线在A站交汇,且两条地铁线互相垂直如图所示,学校P到地铁一号线B站的距离PB=2km,到地铁二号线C站的距离PC为4km,PB与一号线的夹角为30°,PC与二号线的夹角为60°.求学校P到A站的距离(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林城市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
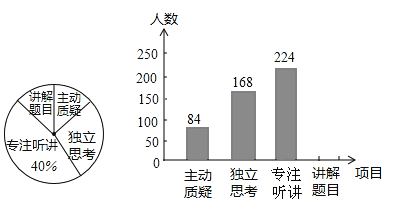
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com