
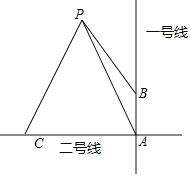
【题目】合肥地铁一号线与地铁二号线在A站交汇,且两条地铁线互相垂直如图所示,学校P到地铁一号线B站的距离PB=2km,到地铁二号线C站的距离PC为4km,PB与一号线的夹角为30°,PC与二号线的夹角为60°.求学校P到A站的距离(结果保留根号)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形OABC的边OC=2,将过点B的直线y=x﹣3与x轴交于点E.
(1)求点B的坐标;
(2)连结CE,求线段CE的长;
(3)若点P在线段CB上且OP=![]() ,求P点坐标.
,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①已知菱形的两条对角线长分别是a、b,则这个菱形的面积为![]() ab;②在Rt△ABC中,∠C=90°,若∠A>∠B,则cosA<cosB;③若m=n+1,则1﹣m2+2mn﹣n2=0;④若点A(x1,y1)和点B(x2,y2)在二次函数y=x2﹣2x﹣1的图象上,且满足x1>x2>1,则y2>y1>﹣2;其中假命题的个数是( )
ab;②在Rt△ABC中,∠C=90°,若∠A>∠B,则cosA<cosB;③若m=n+1,则1﹣m2+2mn﹣n2=0;④若点A(x1,y1)和点B(x2,y2)在二次函数y=x2﹣2x﹣1的图象上,且满足x1>x2>1,则y2>y1>﹣2;其中假命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
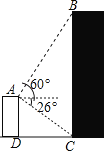
【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:![]() ≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
查看答案和解析>>
科目:初中数学 来源: 题型:
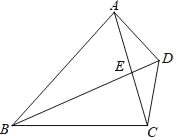
【题目】已知:如图,四边形ABCD的对角线AC和BD相交于点E,AD=DC,DC2=DEDB,求证:
(1)△BCE∽△ADE;
(2)ABBC=BDBE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
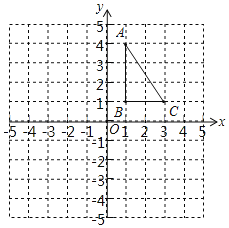
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC绕O点顺时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求点C划过的路径长度(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
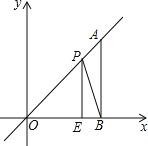
A.4+2![]() B.4+
B.4+![]() C.6D.4
C.6D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图象与性质,探究过程如下,请补充完整.
的图象与性质,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ,
,![]() ;
;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
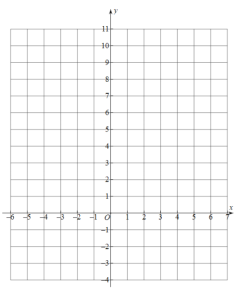
(3)观察函数图象:
①当方程![]() 有且仅有两个不相等的实数根,根据函数图象直接写出
有且仅有两个不相等的实数根,根据函数图象直接写出![]() 的取值范围为 ;
的取值范围为 ;
②在该平面直角坐标系中画出直线![]() 的图象,根据图象直接写出该直线与函数
的图象,根据图象直接写出该直线与函数![]()
![]() 的交点横坐标为: (结果保留一位小数).
的交点横坐标为: (结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过抛物线y=ax2+bx上一点A(4,﹣2)作x轴的平行线,交抛物线于另一点B,点C在直线AB上,抛物线交x轴正半轴于点D(2,0),点B与点E关于直线CD对称.
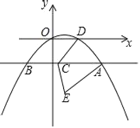
(1)求抛物线的表达式;
(2)①若点E落在抛物线的对称轴上,且在x轴下方时,求点C的坐标.②AE最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com