
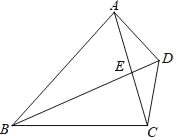
【题目】已知:如图,四边形ABCD的对角线AC和BD相交于点E,AD=DC,DC2=DEDB,求证:
(1)△BCE∽△ADE;
(2)ABBC=BDBE.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由∠DAC=∠DCA,对顶角∠AED=∠BEC,可证△BCE∽△ADE.
(2)根据相似三角形判定得出△ADE∽△BDA,进而得出△BCE∽△BDA,利用相似三角形的性质解答即可.
证明:(1)∵AD=DC,
∴∠DAC=∠DCA,
∵DC2=DEDB,
∴![]() =
=![]() ,∵∠CDE=∠BDC,
,∵∠CDE=∠BDC,
∴△CDE∽△BDC,
∴∠DCE=∠DBC,
∴∠DAE=∠EBC,
∵∠AED=∠BEC,
∴△BCE∽△ADE,
(2)∵DC2=DEDB,AD=DC
∴AD2=DEDB,
同法可得△ADE∽△BDA,
∴∠DAE=∠ABD=∠EBC,
∵△BCE∽△ADE,
∴∠ADE=∠BCE,
∴△BCE∽△BDA,
∴![]() =
=![]() ,
,
∴ABBC=BDBE.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G。
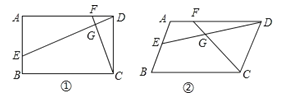
(1)如图①,若AB∥CD,AB=CD,∠A=90°,且AD·DF=AE·DC,求证:DE⊥CF;
(2)如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DE·CD=CF·DA.
查看答案和解析>>
科目:初中数学 来源: 题型:
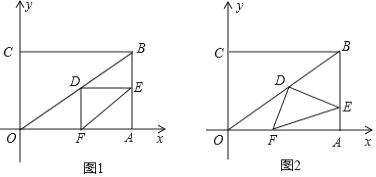
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连接OB,点D为OB的中点,点E是线段AB上的动点,连接DE,作DF⊥DE,交OA于点F,连接EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,![]() 的大小是否发生变化?如果变化,请说明理由;如果不变,请求出
的大小是否发生变化?如果变化,请说明理由;如果不变,请求出![]() 的值.
的值.
(3)连接AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
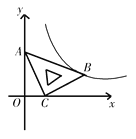
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),AB=![]() ,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,△
中,△![]() 的顶点
的顶点![]() 、
、![]() 在坐标轴上,点
在坐标轴上,点![]() 的坐标是(2,2).将△ABC沿
的坐标是(2,2).将△ABC沿![]() 轴向左平移得到△A1B1C1,点
轴向左平移得到△A1B1C1,点![]() 落在函数y=-
落在函数y=-![]() .如果此时四边形
.如果此时四边形![]() 的面积等于
的面积等于![]() ,那么点
,那么点![]() 的坐标是________.
的坐标是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对学校饭菜的满意程度,某中学数学兴趣小组对在校就餐的学生进行了抽样调查,得到如下不完整的统计图.

请结合图中信息,解决下列问题:
(1)此次调查中接受调查的人数为人,其中“非常满意”的人数为_ _
(2)兴趣小组准备从“不满意”的4位学生中随机抽取2位进行回访,已知这4位学生中有2位男生2位女生,请用列举法求出随机抽取的学生是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com