
【题目】已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G。
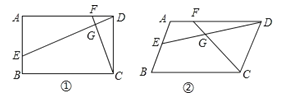
(1)如图①,若AB∥CD,AB=CD,∠A=90°,且AD·DF=AE·DC,求证:DE⊥CF;
(2)如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DE·CD=CF·DA.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据已知条件得到四边形ABCD是矩形,由矩形的性质得到∠A=∠FDC=90°,根据相似三角形的性质得到∠CFD=∠AED,根据余角的性质即可得到结论;
(2)根据已知条件得到△DFG∽△DEA,推出![]() ,根据△CGD∽△CDF,得到
,根据△CGD∽△CDF,得到![]() ,等量代换即可得到结论;
,等量代换即可得到结论;
(1)证明:∵AB∥CD,AB=CD,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠FDC=90°,
∵ADDF=AEDC,
∴![]() ,
,
∴△AED∽△DFC,
∴∠CFD=∠AED,
∵∠ADE+∠AED=90°,
∴∠ADE+∠CFD=90°,
∴∠DGF=90°,
∴DE⊥CF;
(2)证明:∵∠A=∠EGC,∠ADE=∠GDF,
∴△DFG∽△DEA,
∴![]() =
=![]() ,
,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,∠AED=∠EDC,
∴∠B=∠ADC,
∵△DFG∽△DEA,
∴∠AED=∠DFG,
∴∠DFC=∠GDC,
∵∠DCG=∠FCD,
∴△CGD∽△CDF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴DECD=CFDA;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(4,2),点B在第一象限,AB平行于x轴且AB=5.
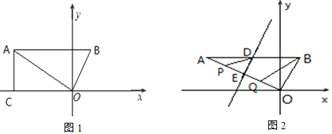
(1)点B的坐标为_______.
(2)如图1,过点A作AC⊥x轴于C,在x轴上是否存在点D,使得△AOC与△BOD相似?
(3)如图2,将△AOB折叠,使得点A刚好落在O处,此时折痕交AB于点D,交AO于点E,在直线AO上有两个动点P,Q(点P在点Q的左侧),且线段PQ=![]() ,求四边形BDPQ的周长最小值.
,求四边形BDPQ的周长最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上一点,
上一点,![]() ,过点
,过点![]() 三点的
三点的![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]()
(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)若![]() ,请用题意可以推出的结论说明命题:“一组对边相等,且一组对角相等的四边形是平行四边形”是假命题
,请用题意可以推出的结论说明命题:“一组对边相等,且一组对角相等的四边形是平行四边形”是假命题

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解本校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,课题小组随机选取该校部分学生进行了问卷调査(问卷调査表如图所示),并根据调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答下列问题.
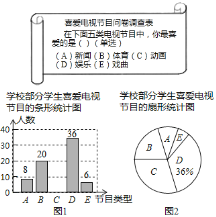
(1)本次接受问卷调查的学生有____名.
(2)补全条形统计图.
(3)扇形统计图中B类节目对应扇形的圆心角的度数为_____.
(4)该校共有4000名学生,根据调查结果估计该校最喜爱新闻节目的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
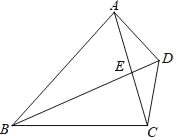
【题目】已知:如图,四边形ABCD的对角线AC和BD相交于点E,AD=DC,DC2=DEDB,求证:
(1)△BCE∽△ADE;
(2)ABBC=BDBE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy(如图),抛物线y=﹣x2+2mx+3m2(m>0)与x轴交于点A、B(点A在点B左侧),与y轴交于点C,顶点为D,对称轴为直线l,过点C作直线l的垂线,垂足为点E,联结DC、BC.
(1)当点C(0,3)时,
①求这条抛物线的表达式和顶点坐标;
②求证:∠DCE=∠BCE;
(2)当CB平分∠DCO时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com