
【题目】如图,在平面直角坐标系中,点A(4,2),点B在第一象限,AB平行于x轴且AB=5.
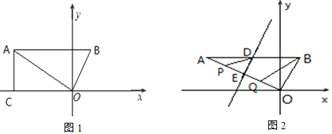
(1)点B的坐标为_______.
(2)如图1,过点A作AC⊥x轴于C,在x轴上是否存在点D,使得△AOC与△BOD相似?
(3)如图2,将△AOB折叠,使得点A刚好落在O处,此时折痕交AB于点D,交AO于点E,在直线AO上有两个动点P,Q(点P在点Q的左侧),且线段PQ=![]() ,求四边形BDPQ的周长最小值.
,求四边形BDPQ的周长最小值.
【答案】(1)(1,2);(2)存在,D(1,0)或(5,0);(3)周长最小值为![]()
【解析】
(1)由AB//x轴可得点B纵坐标,根据AB=5可求出得B横坐标,即可得到答案;(2)根据A、B两点坐标可求出OA、OB的长,根据勾股定理逆定理可得△AOB是直角三角形,∠AOB=90°,当点D在x轴负半轴时,∠BOD>90°,不能与Rt△AOC相似;当点D在x轴正半轴时,根据同角的余角相等可得∠CAO=∠DOB,分别讨论∠OBD=90°和∠ODB=90°两种情况,求出点D坐标即可;(3)由折叠性质可得DE⊥OA,OE=![]() OA=
OA=![]() ,由OB⊥OA可得DE//BO,DE和OB是DP和BQ的最小值,由点E是OA中点DE是△AOB的中位线,可得BD=
,由OB⊥OA可得DE//BO,DE和OB是DP和BQ的最小值,由点E是OA中点DE是△AOB的中位线,可得BD=![]() AB,DE=
AB,DE=![]() OB,进而求出四边形DEOB的周长即可得答案.
OB,进而求出四边形DEOB的周长即可得答案.
(1)∵AB//x轴,A(-4,2),
∴点B的纵坐标为2,
∵AB=5,
∴点B的横坐标为-4+5=1,
∴点B坐标为(1,2).
故答案为:(1,2)
(2)∵A(-4,2),B(1,2),
∴OA=2![]() ,OB=
,OB=![]() ,
,
∵AB2=25,OA2=20,OB2=5,
∴AB2=OA2+OB2,
∴△OAB是直角三角形,∠AOB=90°,
当点D在x轴负半轴时,∠BOD>90°,不能与Rt△AOC相似;
当点D在x轴正半轴时,
∵∠AOC+∠BOD=90°,∠AOC+∠CAO=90°,
∴∠CAO=∠DOB,
如图,当∠OBD2=90°时,
∵∠D2OB=∠CAO,∠OBD2=∠ACO=90°,
∴△OBD2∽△ACO,
∴![]() ,即
,即![]() ,
,
∴OD2=5,
∴D2(5,0).
当∠OD1B=90°时,
∵∠BOD1=∠CAO,∠OD1B=∠ACO=90°,
∴△BOD1∽△OAC,
∵∠OD1B=90°,B(1,2)
∴OD1=1,
∴D1(1,0)

综上所述:存在点D,使得△AOC与△BOD相似,点D坐标为(1,0)或(5,0).
(3)∵将△AOB折叠,使得点A刚好落在O处,此时折痕交AB于点D,交AO于点E,
∴DE⊥OA,AE=OE=![]() OA=
OA=![]()
∵∠AOB=90°,
∴DE//OB,
∴AD=BD=![]() AB=
AB=![]() ,
,
∴DE是△AOB的中位线,
∴DE=![]() OB=
OB=![]() ,
,
∵DE⊥OA,OB⊥OA,OE=![]() ,
,
∴DE和BO即是DP和BQ的最小值,
∴四边形BDPQ的周长最小值为BD+DE+OE+OB=![]() +
+![]() +
+![]() +
+![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一种进价为每件40元的T恤,若销售单价为60元,则每周可卖出300件.为提高利润,欲对该T恤进行涨价销售.经过调查发现:每涨价1元,每周要少卖出10件.请确定该T恤涨价后每周的销售利润y(元)与销售单价x(元)之间的函数关系式,并求销售单价定为多少元时,每周的销售利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
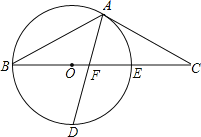
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF=![]() ,求⊙O的半径r.
,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现
如图1,在五边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,试猜想
,试猜想![]() ,
,![]() ,
,![]() 之间的数量关.小明地过仔细思考,得到如下解题思路:
之间的数量关.小明地过仔细思考,得到如下解题思路:
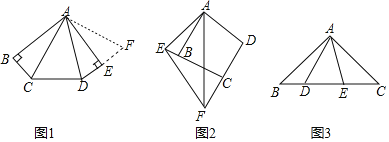
将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() .由
.由![]() ,得
,得![]() ,即点
,即点![]() ,
,![]() ,
,![]() 三点共线,易证
三点共线,易证![]() _____,被
_____,被![]() ,
,![]() ,
,![]() 之间的数量关系是_______;
之间的数量关系是_______;
(2)类比探究
如图2,在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 的延长线上,
的延长线上,![]() ,连接
,连接![]() ,试猜想
,试猜想![]() ,
,![]() ,
,![]() 之间的数量关系,并给出证明.
之间的数量关系,并给出证明.
(3)拓展延伸
如图3,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 均在边
均在边![]() 上,且
上,且![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为_____.
的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
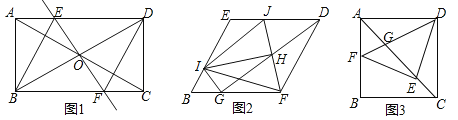
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:

下列说法正确的是( )
A. 抛物线的开口向下
B. 当x>-3时,y随x的增大而增大
C. 二次函数的最小值是-2
D. 抛物线的对称轴是x=-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G。
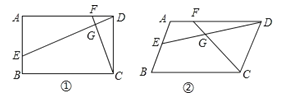
(1)如图①,若AB∥CD,AB=CD,∠A=90°,且AD·DF=AE·DC,求证:DE⊥CF;
(2)如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DE·CD=CF·DA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com