
����Ŀ���߹���ͼ���е�������ʹ�����˳������У�������߳����Ƶ�������Ҳ�����⣬���ǿ���ֻ��Բ�潫Բ�ȷ֣�����ɽ�Բ6�ȷ֣���ͼֻ���ڡ�O����ȡ��A���ӵ�A��ʼ���ԡ�O�İ뾶Ϊ�뾶���ڡ�O�����ν�ȡ��B��C��D��E��F���Ӷ���A��B��C��D��E��F�ѡ�O���ȷ֣����п���ֻ��Բ��ȷֵ��ǣ� �� �����ȷ� �����ȷ� ���ĵȷ� ����ȷ֣�
A.��
B.�٢�
C.�٢ڢ�
D.�٢ڢۢ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2��ͼ���㣨2��1����
��1������κ���y=ax2�Ľ���ʽ��
��2��һ�κ���y=mx+4��ͼ������κ���y=ax2��ͼ���ڵ�A��x1��y1����B��x2��y2�����㣮
�ٵ�m=![]() ʱ��ͼ�٣�����֤����AOBΪֱ�������Σ�
ʱ��ͼ�٣�����֤����AOBΪֱ�������Σ�
�����жϵ�m��![]() ʱ��ͼ�ڣ�����AOB����״����֤���� n>S����DOE��ü��ɣ�
ʱ��ͼ�ڣ�����AOB����״����֤���� n>S����DOE��ü��ɣ�
��3�����ݵ�2�ʣ�˵��һ�����ܵõ��Ľ��ۣ�����Ҫ��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB�㣬AB=5��BC=3��P��AB���ϵĶ��㣨�����B�غϣ�������BCP��CP���ڵ�ֱ�߷��ۣ��õ���B��CP������B��A����B��A���ȵ���Сֵ�� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ز���÷�����ļ��ڣ�ijˮ�������̵�������δ������г���������÷40�䣬��֪��һ�����ν����۷ֱ�Ϊÿ��50Ԫ��40Ԫ���ҵڶ��αȵ�һ�ζึ��700Ԫ��
��1�����һ�����ι�����÷�������ֱ�Ϊa�䡢b�䣬��a��b��ֵ��
��2�����̵����40����÷�Ȱ�ÿ��60Ԫ������x�䣬����İ�ÿ��35Ԫȫ�����꣮
�����̵�������ȫ����÷��������y��Ԫ����x���䣩֮��ĺ�����ϵʽ��
�ڵ�x��ֵ����Ϊ����ʱ���̵�Ų��������
��ע����������ۣ�����=���������멁�����ܳɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�������ı���![]() �ĵ��������ν����ƽ���������Σ�
�ĵ��������ν����ƽ���������Σ�
��ͼ����֪��ABC�У�AC=BC����C=36�㣬BA1ƽ�֡�ABC��AC��A1 �� 
��1��֤����AB2=AA1AC��
��2��̽������ABC�Ƿ�Ϊ�ƽ���������Σ���˵�����ɣ�����ʾ���˴�������AC=1��
��3��Ӧ�ã���֪AC=a����A1B1��AB��BC��B1 �� B1A2ƽ�֡�A1B1C��AC��A2 �� ��A2B2��AB��B2 �� B2A3ƽ�֡�A2B2C��AC��A3 �� ��A3B3��AB��BC��B3 �� �������˹��ɲ�����ȥ���ú�a��n�Ĵ���ʽ��ʾAn��1An �� ��nΪ����1��������ֱ�ӻش𣬲���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=AD=6��AB��BC��AD��CD����BAD=60�㣬��M��N�ֱ���AB��AD���ϣ���AM��MB=AN��ND=1��2���� cos��MCN= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ߳�Ϊ1��С��������ɵ������������н�����ͼƬ��ʾ��ƽ��ֱ������ϵ����֪���������ABC�������ε��������㶼��С�������ϣ�
��1��������ABC����ֱ��l��x=��1�ĶԳ������Ρ�A1B1C1����д��A1��B1��C1�����꣮
��2����ֱ��x=��l����һ��D��ʹBD+CD��С������������D��Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�γ������ᄊ�˶����ϣ����ݲμ��������߳������˶�Ա�ijɼ�����λ��m�������Ƴ����µ�ͳ��ͼ�ٺ�ͼ�ڣ�����������Ϣ������������⣺ 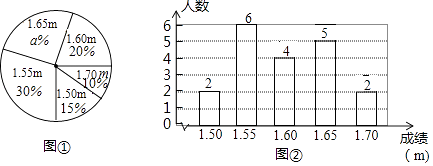
��1������a��ֵΪ��
��2��ͳ�Ƶ���������ɼ����ݵ�ƽ��������������λ�����������С�������λ����
��3������������ɼ����ɸߵ���ȷ��7�˽��븴������ֱ��д�������ɼ�Ϊ1.60m���˶�Ա�ܷ���븴����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ƽ��ֱ������ϵ�У�ֱ��y=kx+b��x�ύ�ڵ�A��6��0������y�ύ�ڵ�B����ֱ��y=2x���ڵ�C��a��4����
��1�����C�����꼰ֱ��AB�ı���ʽ��
��2����ͼ2���ڣ�1���������£�����E��ֱ��l��x���ڵ�E����ֱ��y=2x�ڵ�F����ֱ��y=kx+b�ڵ�G������E�������ǣ�4��0����
������CGF�������
��ֱ��l���Ƿ���ڵ�P��ʹOP+BP��ֵ��С�������ڣ�ֱ��д����P�����ꣻ�������ڣ�˵�����ɣ�
��3������2���еĵ�E��x���ϵ�һ�����㣬��E�ĺ�����Ϊm��m��0��������E��x�����˶�ʱ��̽���������⣺
��mȡ��ֵʱ��ֱ��l�ϴ��ڵ�Q��ʹ����A��C��QΪ���������������AOCȫ�ȣ���ֱ��д����Ӧ��m��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com