
【题目】(1)阅读理解:
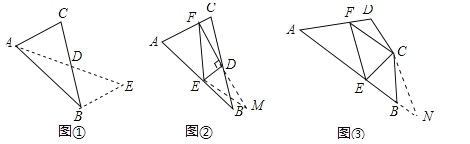
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

【答案】(1)2<AD<8;(2)证明见解析;(3)BE+DF=EF.
【解析】
试题分析:(1)延长AD至E,使DE=AD,由SAS证明△ACD≌△EBD,得出BE=AC=6,在△ABE中,由三角形的三边关系求出AE的取值范围,即可得出AD的取值范围;
(2)延长FD至点M,使DM=DF,连接BM、EM,同(1)得△BMD≌△CFD,得出BM=CF,由线段垂直平分线的性质得出EM=EF,在△BME中,由三角形的三边关系得出BE+BM>EM即可得出结论;
(3)延长AB至点N,使BN=DF,连接CN,证出∠NBC=∠D,由SAS证明△NBC≌△FDC,得出CN=CF,∠NCB=∠FCD,证出∠ECN=70°=∠ECF,再由SAS证明△NCE≌△FCE,得出EN=EF,即可得出结论.
试题解析:(1)解:延长AD至E,使DE=AD,连接BE,如图①所示:
∵AD是BC边上的中线,∴BD=CD,在△BDE和△CDA中,∵BD=CD,∠BDE=∠CDA,DE=AD,∴△BDE≌△CDA(SAS),∴BE=AC=6,在△ABE中,由三角形的三边关系得:AB﹣BE<AE<AB+BE,∴10﹣6<AE<10+6,即4<AE<16,∴2<AD<8;
故答案为:2<AD<8;
(2)证明:延长FD至点M,使DM=DF,连接BM、EM,如图②所示:
同(1)得:△BMD≌△CFD(SAS),∴BM=CF,∵DE⊥DF,DM=DF,∴EM=EF,在△BME中,由三角形的三边关系得:BE+BM>EM,∴BE+CF>EF;
(3)解:BE+DF=EF;理由如下:
延长AB至点N,使BN=DF,连接CN,如图3所示:
∵∠ABC+∠D=180°,∠NBC+∠ABC=180°,∴∠NBC=∠D,在△NBC和△FDC中,∵BN=DF,∠NBC=∠D,BC=DC,∴△NBC≌△FDC(SAS),∴CN=CF,∠NCB=∠FCD,∵∠BCD=140°,∠ECF=70°,∴∠BCE+∠FCD=70°,∴∠ECN=70°=∠ECF,在△NCE和△FCE中,∵CN=CF,∠ECN=∠ECF,CE=CE,∴△NCE≌△FCE(SAS),∴EN=EF,∵BE+BN=EN,∴BE+DF=EF.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,轮船沿正南方向以33海里/时的速度匀速航行,在m处观测到灯塔p在西偏南69°方向下,航行2小时后到达n处,观测灯塔p在西偏南57°方向上,若该船继续向南航行至离灯塔最近位置,求此时轮船离灯塔的距离约为多少海里?(结果精确到整数,参考数据:tan33°≈ ![]() ,sin33°≈
,sin33°≈ ![]() ,cos33°≈
,cos33°≈ ![]() ,tan21°≈
,tan21°≈ ![]() ,sin21°≈
,sin21°≈ ![]() ,c0s21°≈
,c0s21°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,把直角三角形![]() 的直角顶点
的直角顶点![]() 放在直线
放在直线![]() 上,射线
上,射线![]() 平分
平分![]() .
.
(1)如图,若![]() ,求
,求![]() 的度数.
的度数.
(2)若![]() ,则
,则![]() 的度数为 .
的度数为 .
(3)由(1)和(2),我们发现![]() 和
和![]() 之间有什么样的数量关系?
之间有什么样的数量关系?
(4)若将三角形![]() 绕点
绕点![]() 旋转到如图所示的位置,试问
旋转到如图所示的位置,试问![]() 和
和![]() 之间的数量关系是否发生变化?请说明理由.
之间的数量关系是否发生变化?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了研究,下面是小慧的研究过程,请补充完成:
(1)函数y=|x﹣1|的自变量x的取值范围是 ;
(2)列表,找出y与x的几组对应值.其中,b= ;
x | … | ﹣1 | 0 | 2 | 3 | … | |
y | … | b | 0 | 2 | … |
(3)在平面直角坐标系xoy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着几何部分的学习,小鹏对几何产生了浓厚的兴趣,他最喜欢利用手中的工具画图了![]() 如图,作一个
如图,作一个![]() ,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接
,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接![]() 小鹏通过观察和推理,得出结论:OP平分
小鹏通过观察和推理,得出结论:OP平分![]() .
.
你同意小鹏的观点吗?如果你同意小鹏的观点,试结合题意写出已知和求证,并证明.
已知:![]() 中,______
中,______![]() ______,______
______,______![]() ______,______
______,______![]() ______.
______.
求证:OP平分![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别为(-2,-2),(3,1),(0,2),若把三角形ABC向上平移 3 个单位长度,再向左平移 ![]() 个单位长度得到三角形
个单位长度得到三角形 ![]() ,点A,B,C的对应点分别为
,点A,B,C的对应点分别为 ![]() ,
,![]() ,
,![]() .
.
(1)写出点 ![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)在图中画出平移后的三角形 ![]() ;
;
(3)三角形 ![]() 的面积为__________.
的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为 ( ).

A. 70°B. 75°C. 80°D. 85°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com