
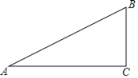
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°.
(1)作线段AB的垂直平分线DE,垂足为点E,交AC于点D,要求用尺规作图,保留作图痕迹,标注有关字母,不要求写作法和证明;
(2)连接BD,直接写出∠CBD的度数;
(3)如果△BCD的面积为4,请求出△BAD的面积.
【答案】(1)详见解析;(2)30°;(3)8.
【解析】
(1)利用基本作图,作AB的垂直平分线即可;
(2)利用垂直平分线的性质得DA=DB,则∠DBA=∠A=30°,然后计算∠ABC-∠DBA即可;
(3)在Rt△BCD中利用含30度的直角三角形三边的关系得到DB=2CD,则DA=2CD,然后根据三角形面积公式得到S△ABD=2S△BCD=8.
(1)如图,DE为所作;
(2)∵DE垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=30°,
∵∠ABC=90°﹣∠A=60°,
∴∠CBD=∠ABC﹣∠DBA=60°﹣30°=30°;
(3)在Rt△BCD中,∵∠CBD=30°,
∴DB=2CD,
而DA=DB,
∴DA=2CD,
∴S△ABD=2S△BCD=8.


科目:初中数学 来源: 题型:
【题目】下列说法中,①任意有理数![]() 的倒数是
的倒数是![]() ,②相反数等于自身的数只有一个,③海拔-155米表示海平面下155米,④绝对值大于本身的数一定是负数,⑤零是最小的自然数,⑥有理数包含正有理数和负有理数,⑦任意有理数
,②相反数等于自身的数只有一个,③海拔-155米表示海平面下155米,④绝对值大于本身的数一定是负数,⑤零是最小的自然数,⑥有理数包含正有理数和负有理数,⑦任意有理数![]() 的相反数是
的相反数是![]() .正确的有( )个
.正确的有( )个
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
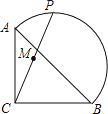
【题目】如图,在等腰RtABC中,![]() ,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
A. ![]() B. 2
B. 2![]() C.
C. ![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
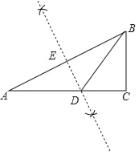
【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
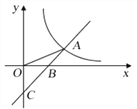
【题目】如图,直线![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于点B,与反比例函数
轴交于点B,与反比例函数![]() 的图象在第一象限交于点A,连接OA,且
的图象在第一象限交于点A,连接OA,且![]() .
.
(1)求ΔBOC的面积.
(2)求点A的坐标和反比例函数![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数3.3 ,-2 ,0 ,![]() ,-3.5 ;
,-3.5 ;
(1) 比较这些数的绝对值的大小,并将这些数的绝对值用“>”号连接起来;
(2) 比较这些数的相反数的大小,并将这些数的相反数用“<”号连接起来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com