
【题目】如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B分别落在x轴、y轴上且AB=12cm
(1)若OB=6cm.
①求点C的坐标;
②若点A向右滑动的距离与点B向上滑动的距离相等,求滑动的距离;
(2)点C与点O的距离的最大值是多少cm.

【答案】(1)①点C的坐标为(-3![]() ,9);②滑动的距离为6(
,9);②滑动的距离为6(![]() ﹣1)cm;(2)OC最大值12cm.
﹣1)cm;(2)OC最大值12cm.
【解析】
试题(1)①过点C作y轴的垂线,垂足为D,根据30°的直角三角形的性质解答即可;②设点A向右滑动的距离为x,根据题意得点B向上滑动的距离也为x,根据锐角三角函数和勾股定理解答即可;(2)设点C的坐标为(x,y),过C作CE⊥x轴,CD⊥y轴,垂足分别为E,D,证得△ACE∽△BCD,利用相似三角形的性质解答即可.
试题解析:解:(1)①过点C作y轴的垂线,垂足为D,如图1:
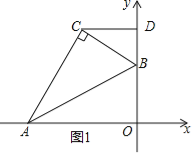
在Rt△AOB中,AB=12,OB=6,则BC=6,
∴∠BAO=30°,∠ABO=60°,
又∵∠CBA=60°,∴∠CBD=60°,∠BCD=30°,
∴BD=3,CD=3![]() ,
,
所以点C的坐标为(﹣3![]() ,9);
,9);
②设点A向右滑动的距离为x,根据题意得点B向上滑动的距离也为x,如图2:
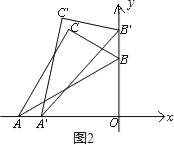
AO=12×cos∠BAO=12×cos30°=6![]() .
.
∴A'O=6![]() ﹣x,B'O=6+x,A'B'=AB=12
﹣x,B'O=6+x,A'B'=AB=12
在△A'O B'中,由勾股定理得,
(6![]() ﹣x)2+(6+x)2=122,解得:x=6(
﹣x)2+(6+x)2=122,解得:x=6(![]() ﹣1),
﹣1),
∴滑动的距离为6(![]() ﹣1);
﹣1);
(2)设点C的坐标为(x,y),过C作CE⊥x轴,CD⊥y轴,垂足分别为E,D,如图3:
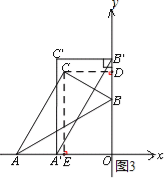
则OE=﹣x,OD=y,
∵∠ACE+∠BCE=90°,∠DCB+∠BCE=90°,
∴∠ACE=∠DCB,又∵∠AEC=∠BDC=90°,
∴△ACE∽△BCD,
∴![]() ,即
,即![]() ,
,
∴y=﹣![]() x,
x,
OC2=x2+y2=x2+(﹣![]() x)2=4x2,
x)2=4x2,
∴当|x|取最大值时,即C到y轴距离最大时,OC2有最大值,即OC取最大值,如图,即当C'B'旋转到与y轴垂直时.此时OC=12,
故答案为:12.


科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100
B.x2+8x+9=0化为(x+4)2=25
C.2t2﹣7t﹣4=0化为(t﹣![]() )2=
)2=![]()
D.3x2﹣4x﹣2=0化为(x﹣![]() )2=
)2=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为正方形ABCD的边CD上一点,BP的垂直平分线EF分别交BC、AD于E、F两点,GP⊥EP交AD于点G,连接BG交EF于点 H,下列结论:①BP=EF;②∠FHG=45°;③以BA为半径⊙B与GP相切;④若G为AD的中点,则DP=2CP.其中正确结论的序号是( )
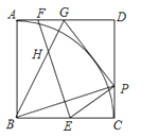
A. ①②③④ B. 只有①②③ C. 只有①②④ D. 只有①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.
下列四种说法:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.
其中,正确的有( ) 个.

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队同时挖掘两段长度相等的隧道,如图是甲、乙两队挖掘隧道长度![]() (米)与挖掘时间
(米)与挖掘时间![]() (时)之间关系的部分图象.请解答下列问题:
(时)之间关系的部分图象.请解答下列问题:
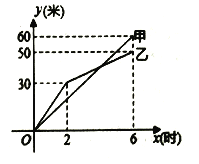
![]() 在前
在前![]() 小时的挖掘中,甲队的挖掘速度为 米/小时,乙队的挖掘速度为 米/小时.
小时的挖掘中,甲队的挖掘速度为 米/小时,乙队的挖掘速度为 米/小时.
![]() ①当
①当![]() 时,求出
时,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
②开挖几小时后,两工程队挖掘隧道长度相差![]() 米?
米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2020的坐标是( )
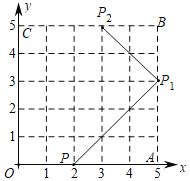
A.(5,3)B.(3,5)C.(0,2)D.(2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示
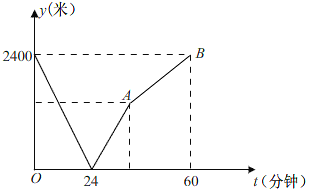
(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟;
(2)求出线段AB所表示的函数表达式
(3)甲、乙两人何时相距400米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位运动员在一段2000米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面200米,他们同时同向出发匀速前进,甲的速度是8米/秒,乙的速度是6米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是y米,比赛时间是x秒,当两人都到达终点计时结束,整个过程中y与之间的函数图象是( )
A.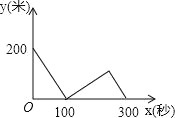 B.
B.
C.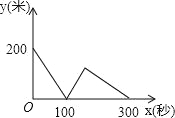 D.
D.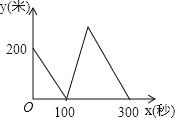
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公路AB和公路CD在点P处交汇,点E处有一所学校,EP=160米,点E到公路AB的距高EF=80米,假若拖拉机行驶时,周围100米内会受到噪音影响,那么拖拉机在公路AB上沿方向行驶时,学校是否受到影响,请说明理由;如果受到影响,已知拖拉机的速度是18千米/小时,那么学校受到影响的时间为多少?
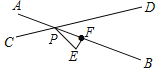
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com